La energía negativiescéptica

Hace poco hablábamos de dos (pseudo)-científicos de la Universidad de Amsterdam, que habían "demostrado" la existencia de la telepatía telefónica.

Bien, ahí no acaba la cosa, porque también han "demostrado" (redoble de tambores)....

La existencia de la energía negativa que emana todo escéptico que se precie

Pues sí. Resulta que hay gente que es capaz de saber cuando alguien le está mirando sin necesidad de establecer contacto visual con el mirón de turno. Afirmación hecha por Rupert Sheldrake, y que por supuesto, es capaz de obtener resultados asombrosos en sus experimentos.

Así que de nuevo Lobach & Bierman, intentan reproducir los resultados (.pdf). Cogen a varias personas, y los colocan en una habitación, donde los observa o no una persona. El observador tiene que decir si le están mirando o no, y se anota si es un fallo o un acierto.

La gran innovación está en que se dividió a los mirones entre "escépticos" y "creyentes". En total, había dos tandas a cada observado en que cada mirón miraba al observado 15 veces y no miraba otras 15 veces por tanda, siendo los resultados finales los siguientes:

Cuando miraba un creyente, la media de aciertos era 7.40±2.39 (49.9%)
Cuando no miraba un creyente, la media de aciertos era 7.19±2.24 (48.5%)
dando un total general de 48.9% de aciertos.

Cuando miraba un escéptico, la media de aciertos era 8.06±2.14 (54.3%)
Cuando no miraba un escéptico, la media de aciertos era 7.51±2.27 (54.3%)
dando un total general de 52.3% de aciertos.

Pues bien, esos 8.06 (±2.14) aciertos de media frente al 7.50 teórico, cuando mira un escéptico son los que dan pie a los autores para concluir que

"la tasa de aciertos cuando mira un escéptico es marginalmente significativa"

o lo que es lo mismo, que nos han descubierto.

¿Por qué no aparecen fenómenos paranormales cuando hay un escéptico presente en la sala? Por la energía negativa que emanamos, y que hace que cualquier fenómeno paranormal se vuelva mundano.

Es la que hace que las naves extraterrestres se conviertan en gases emitidos por misiles. La misma que transforma una auténtica y acojonante fotografía paranormalísima en burdos montajes, que cambia la posición de los bigotes de la Benemérita, y que incluso convierte en chapuceros unos estudios informáticos de comparativa forense o que teleplastias impresionantes se conviertan en una mancha difusa, como si alguien hubiera pasado una fregona pringada en aceite

Así que ya lo saben. Si sus grabadoras no captan psicofonías, si sus pirámides les pudren los filetes de pollo, si los extraterrestres no les quieren abducir, o si sus medicinas homeopáticas no recuerdan como curar la gripe, es porque hay algún escéptico mirando.

Ring, ring ¿quien es?

En una ocasión hablamos de un artículo de El País Semanal, donde hacían un reportaje acerca de Rupert Sheldrake, y sus teorías (por llamarlas de alguna manera), acerca de la telepatía, inconsciente colectivo y demás zarandajas.

Una de sus sorprendentes afirmaciones es que una persona es capaz de saber quién está llamando por teléfono antes de responder. El caso es que hay gente que incluso cree que estas afirmaciones son ciertas más allá de lo esperado por azar, y así, hemos encontrado a dos profesores de psicología de la Universidad de Amsterdam que han intentado replicar experimentos previos de Sheldrake, cuyo resultado se puede leer en un artículo titulado "Who's calling at this hour? Local Sidereal Time and telephone telepathy" (.pdf) ("¿Quién llama a esta hora? Telepatía telefónica y Hora Sidérea Local "), perpetrado por Eva Lobach y Dick Bierman, y publicado en los proceedings una Convención de la Asociación Parapsicológica en 2004.

La afirmación original de Sheldrake es que el hecho de que una persona adivine quien está llamando antes de coger el teléfono no es por azar, sino por telepatía. ¿A quien no le ha pasado que está pensando en alguien, y justo en ese momento esa persona llama por teléfono?. De lo que no se suele acordar la gente es de aquellas veces que la persona que llama no es en quien pensábamos.

Pero ahí no acaba todo. Se supone además que se encontró experimentalmente una correlación entre la hora sidérea local y la capacidad de saber quien llama, habiendo una hora "punta" a eso de las 13.30 (hora sidérea local ).

Así que ni cortos ni perezosos, Lobach & Bierman escogieron 6 personas que decían tener ese tipo de experiencias. Cada una de ellas, escogió 4 amigos o familiares, que les llamarían por teléfono según el azar dictado por un dado lanzado por un experimentador. Antes de coger el teléfono, la persona decía en voz alta quien estaba llamando, cogía el teléfono, y otro experimentador anotaba si era un fallo o un acierto.

Se hicieron 36 intentos para cada persona, repartidos de esta forma : 3 series de 6 intentos en hora punta (un total de 18 intentos), y 3 series de 6 intentos en hora valle (otros 18 intentos), y los resultados fueron los de esta tabla:

que a falta de mayor detalle en cada una las 3 sesiones de 6 intentos, lo tomaremos como que hubo una sesión de 18 intentos en la hora punta, y una sesión de 18 intentos en hora valle a cada persona.

Lo primero que resulta curioso comprobar es que 4+4+2+6+4+6 (hits en non-peak hour) no son 27 sino 26. En fin, un errorcillo de imprenta, suponemos.

Hay dos valores no registrados, debido a que el registro del experimentador que determinaba quien llamaba, y el del que comprobaba el acierto eran distintos en la hora de llamada anotada, pero en el texto nos indican que había sido un acierto (y que así constaba en los registros). Y como somos buenos, vamos a aceptar el acierto.

Hay varias formas de tratar los datos. Una de ellas es considerar que cada persona representa una serie de 18 o 36 intentos de la que ha obtenido un valor, y luego se ha calculado la media de estas 6 series para determinar si existe un efecto real. Este es el enfoque que han escogido los autores, y que vamos a seguir.

Los resultados según esta forma de tratar los datos, es que en total se obtuvo un 29% de aciertos (una media de 10.8 sobre 36 intentos), más que el 25% esperado por azar (una media de 9 sobre 36).

Respecto a la influencia de la hora, se obtiene que en la hora punta la media de aciertos era de 6.33 sobre 18 (35%), y en hora valle 4.5 sobre 18 (25%, que coincide con la media esperada por azar).

Ahora viene la pregunta del millón ¿estos datos se pueden atribuir a una "tirada con suerte" de azar puro y duro, o hay un efecto real de telepatía telefónica?. Para evaluarlo, existen tests que determinan cual es la probabilidad de que el resultado obtenido no haya sido debido a la teoría que se está testando. El más común es el de chi-cuadrado (χ2), pero que con pocas muestras puede ser impreciso. En el artículo usan el test t de Student, más útil para pocas muestras. En ambos casos, de la prueba se obtiene un valor, que se compara con uno que está tabulado en función del número de datos de la estadística experimental (grados de libertad), y del nivel de confianza. Éste nivel de confianza se suele tomar del 95% (p=0.05 o p=0.95 según el lugar que se lea). Si el valor de la prueba es menor que el tabulado, entonces podemos pensar que nuestra teoría no es falsa con un margen de confianza del 95%. En caso contrario, habría que tomar en serio la posibilidad de que la teoría es falsa.

En nuestro caso, la teoría a testar es que los resultados son producidos por azar, y lo que habría que obtener en estos tests es un resultado mayor que los tabulados para pensar que puede existir otra teoría.

El test de chi-cuadrado se puede comprobar que da negativo en los tres casos (hora punta, hora valle y total). El test t de Student en el artículo da un resultado positivo tanto en hora punta como en el total. No hemos podido encontrar una forma de comprobarlo, así que vamos a optar por un análisis más de andar por casa, con menos rigor, pero más ilustrativo.

Podemos agrupar los datos de dos formas: series de 18 intentos, y series de 36 intentos. En cada serie, hay una probablidad de acertar un número determinado de veces. Aunque la cuenta de la vieja nos dice que hay que acertar 4.5 veces para series de 18 intentos (9 para 36), en realidad, nada nos impide acertar 10 veces, y que siga siendo por puro azar. Pero si realizamos un número elevado de series, y anotamos cuantas veces acertamos 1, 2 , 3... o 18 veces, se pueden obtener distribuciones de aciertos tal que así:

Distribución que corresponde estrictamente a lo esperado por azar. De aquí se pueden hallar dos parámetros muy importantes: la media y la desviación.

La media corresponde a lo que calculamos por cuenta de la vieja (4.5 para 18 intentos, 9 para 36), pero también importante es la desviación, que nos indica entre qué valores varía el número de aciertos cada vez que hacemos una prueba, o entre que valores se reparten con mayor frecuencia los aciertos.

Para series de 18 intentos, la media teórica es de 4.5, y la desviación de 1.83 (marcado en la gráfica como el punto con las barras, 4.5 ± 1.83), lo que quiere decir que el 66% de las veces, se acertarán entre 4.5-1.83=2.87 (3 veces) y 4.5+1.83=6.33 (6 veces), y el 95% acertará entre 1 y 8. Para series de 36 intentos, la media teórica es 9 ± 2.6

Sin embargo, en este artículo se han hecho sólo 6 series, lo que parecen pocas, y es fácil obtener resultados de medias que no correspondan a la teórica. Para obtener los valores teóricos, habría que repetir las series un elevado número de veces.

En el caso de las 6 series de 36 intentos, la media determinada es de 10.8 ± 2.13. ¿Es posible obtener este valor sólo por azar?. Para ello, hemos generado por azar valores de 6 series de 36 intentos, y los hemos comparado con la media teórica y la obtenida por Lobach & Bierman:

El punto representa el valor medio, y las líneas representan la desviación a cada lado. Y sí, el valor obtenido experimentalmente se puede obtener sólo por azar. Además, el valor experimental entra dentro del rango de media±desviación teórico, lo que suele ser significativo de que los valores son coherentes con la misma teoría (en este caso, que los valores se obtienen por puro azar).

Igual podemos hacer para las 6 series de 18 intentos, donde se obtenía en la hora punta un valor de 6.33±1.75, y para la hora valle 4.5±1.51:

De la hora valle no hace falta hablar.

En el caso de la hora punta, el valor está justo en el límite de entrar en el rango de 4.5±1.83 teórico, aunque sin embargo, sigue siendo posible encontrar resultados parecidos sólo por azar.

El mayor problema del trabajo de Lobach & Bierman, está en que a pesar de hacer un total de 216 intentos, se han agrupado en sólo 6 series, una por persona, de donde se obtienen los datos. Haciendo tan pocas series se pueden obtener una gran variedad de medias (con sus desviaciones), así que ¿cuál es la probabilidad de haber sacado estas medias sólo por azar o por el contrario, que haya salido porque existe un fenómeno real, desconocido y negado por la malvada ciencia oficial?. Eso es lo que miden los test chi-cuadrado y t de Student de que hemos hablado antes.

Aquí vamos a hacerlo "a lo bruto". Vamos a hacer un número elevado de veces un experimento de 6 series de 18 y 36 intentos, y cada vez, vamos a calcular la media. Luego contamos las veces que ha salido cada media, agrupadas en intervalos de 0.5, es decir, contamos el número de veces que la media sale entre 4 y 4.5, entre 4.5 y 5, etc... Para series de 36 intentos, el resultado es:

Todos los valores obtenidos se distribuyen alrededor de la media verdadera (9), entre 6 y 14. Si en vez de 6 series, hubieran sido 12, 24 o 527 series de 36 intentos, esta distribución hubiera sido más estrecha, es decir, habría menos dispersión en los valores que se pueden obtener como media. En todo caso, el punto experimental resulta tener una probabilidad de un 3% para salir en un experimento sólo por azar, mientras que la media verdadera (9 aciertos), tiene menos del 20% (1 de cada 5) de probabilidad de salir.

Es interesante ver como a pesar de ser lo esperado por azar, es más fácil que salga cualquier otro valor (80%) distinto a la media (20%). Cualquier medida de cualquier experimento se distribuye siempre alrededor de un valor verdadero como el mostrado arriba. Por eso es necesario repetir siempre los experimentos, comprobar si el valor obtenido experimentalmente entra o no dentro de la distribución de valores y determinar la media real. También es importante el diseño del experimento para que la anchura alrededor de la que se distribuyen los valores sea lo más estrecha posible, esto es, tener un experimento con la resolución necesaria. Si de pronto un valor no entrara dentro de la distribución, entonces se podría sospechar que ha habido algún fallo en el experimento, o que la teoría utilizada es incorrecta (en ese orden).

Pero en nuestro caso, el valor de Lobach & Bierman entra dentro de la distribución esperada por azar. Sólo si tras un número elevado de experimentos, los valores se agruparan en torno a este 10.8 en vez del 9 teórico, se podría decir que hay un efecto real. Cómo solo tenemos un dato, no se puede concluir que el efecto exista, porque no hay datos suficientes.

Podemos hacer lo mismo para el caso de 6 series de 18 intentos, donde un valor estaba en el límite de lo esperado por azar:

y se puede ver que mientras un valor (el de la hora valle) está en la media, el otro (hora punta) a pesar de estar cercano al límite, todavía entra dentro de lo esperado por azar. Una vez más, sólo es un punto, y no es posible concluir la existencia del fenómeno, a menos que se repita el experimento un número elevado de veces, y las medias de cada uno se agrupen en torno a 6 aciertos.

Repeticiones por cierto, que implican hacer colaborar a las mismas personas cada vez, y puede que no todas tengan ganas de colaborar tanto. Nadie dijo que investigar fuera fácil, ni cuestión de una tarde.

Las conclusiones

En realidad, el estudio es más chapucero de lo contado aquí. Resulta que a la hora de hacer las llamadas, hubo ocasiones en que no todas las personas que iban a llamar estaban disponibles. Es decir, había veces que mientras que la persona llamada intentaba adivinar entre 4 personas distintas, en realidad sólo recibía llamadas de 2 personas porque las otras estaban en la ducha, o dumiendo. Y hubo dos resultados que se anularon por problemas en los registros (aunque aquí los hemos considerado válidos). Esto hace que los valores no sean comparables entre sí y haya que hacer "ingeniería combinacional" para relacionarlos.

Por otro lado, el diseño del experimento tampoco es del todo acertado. Ante todo, se presupone que las personas tienen la misma capacidad de adivinar quien les está llamando. Imaginemos que una de ellas sí tiene esta capacidad, pero las otras 5 no. Al considerar todos los resultados juntos, en realidad se está "ocultando" la capacidad de esa persona entre el "ruido" aleatorio de las otras 5. Lo correcto hubiera sido hacer muchas series, de muchos intentos a cada persona por separado, y no una sola serie de 18 o 36 intentos, según se interpreten los datos, para determinar si esa persona tiene o no la capacidad.

Pero todo esto no es obstáculo para que los autores concluyan que:

"Los resultados muestran una débil evidencia para apoyar la hipótesis de que la Hora Local Sideral afecta a un fenómeno de cognición anómala como la telepatía telefónica. Nuestra muestra era pequeña, y el alto número de sesiones con irregularidades debilitaron aún más la potencia de nuestros análisis. Sin embargo, los resultados son prometedores y se garantiza que habrá réplicas de ellos.

(...)

Los resultados apoyan la existencia de la telepatía telefónica. En general, nuestros participantes acertaron correctamente más de lo esperado por azar. La evidencia no es tan impresionante como el 45% de Sheldrake(2003), sin embargo puede ser debido a su preselección de participantes a través de un estudio previo, mientras que nosotros empleamos un criterio de selección flexible incluyendo sólo a aquellos participantes que declararon haber tenido experiencias de telepatía telefónica en el pasado"

que traducido al castellano, viene a decir:

"Los resultados son pobres porque la muestra era pequeña, la mayoría de series presentaban irregularidades, y ni siquiera sé a ciencia cierta si los participantes tenían la capacidad que decían, por lo que un análisis puede dar cualquier cosa; pero como ha dado un resultado que me gusta a mí, la hipótesis queda apoyada."

Difracción, OVNIs y energía piramidal

Si entre mis lectores se encuentra algún habitual de Curioso Pero Inútil (CPI), sabrá que he estado ausente por motivos laborales. Pero, aquí estamos ya de vuelta, después de haber compartido con la primera parte contratante de CPI unos agradables días en los USA, que me han servido para confirmar que, a excepción de los tiros y las persecuciones de coches, el país es exactamente igual a las películas, (including the typical Mejor-No-Preguntes style hot dogs)

Como en todo viaje, son varias las anécdotas y curiosidades que te vas encontrando, y he aquí una de ellas. En el vuelo de regreso de Guachintón a Niu Yor para enlazar con el vuelo a Madrid, pude cazar esta bonita foto:

Los más imaginativos rápidamente dirán que es una nave espacial extraterrestre tripulada por ganimedianos dispuestos a abducir a quien se ponga a tiro. Más aún si digo que este presunto OVNI "voló paralelo" al avión un rato.

En realidad es un efecto óptico llamado gloria. Se produce por difracción de la luz del sol en torno al avión, y que se proyecta sobre las nubes, convenientemente cercanas para poder apreciar el efecto.

Imagina una rendija, por la que pasa un haz de luz. Cuando llega el haz a la rendija, se comporta como si desde cada punto de la rendija re-emitiera una nueva onda de luz, que se expande como una esfera.

En el dibujo, cada raya representa un máximo de la amplitud de la onda. Antes de la rendija la onda viaja en una sola dirección. Después de la rendija, viaja expandiéndose como una esfera. Esto es llamado el principio de Huygens.

Si en vez de una rendija, tenemos un objeto opaco, esto mismo ocurre en sus bordes.

Cada color del dibujo representa una onda re-emitida por cada uno de los bordes del objeto, según el principio de Huygens. Al expandirse, llega un momento en que coinciden en el mismo punto del espacio. Entonces, interfieren: cuando coinciden dos máximos o dos mínimos de la amplitud, las intensidades de las ondas se suman. Pero si coinciden el máximo y el mínimo de la otra, entonces el resultado es cero. Cualquier otra coincidencia es un caso intermedio, y dará menos intensidad que la suma de ambas ondas.

Si colocamos un papel o pantalla donde proyectar la luz que está interfiriendo, al final se obtiene un patrón de interferencia, que son una serie de franjas de intensidad, donde debería aparecer nada más que una sombra. Este patrón depende del tamaño del objeto, de la distancia a la pantalla, y también del color de la luz. Si el haz tiene una sola longitud de onda (color), las franjas que aparecen son del mismo color que el haz original. Si en cambio tenemos luz blanca como la del sol, que es mezcla de todos los colores, en vez de franjas con distinta luminosidad se obtiene una separación de los colores, como se puede apreciar en la foto desde el avión.


Y aquí una foto del pasado eclipse del 3 de Octubre. La foto la hice con un tubo de PVC con un agujero muy pequeño (así a ojo, menos de un milímetro de diámetro), adaptado a una cámara reflex, de forma que funcionara como "cámara oscura". Si bien la imagen no fue todo lo bonita que hubiera deseado, sí queda al menos curiosa, ya que se ve muy bien el fenómeno de difracción en el agujero del PVC, y en vez de franjas, aparecen anillos de distinta luminosidad.

¿Y eso para qué sirve?

Y ahora la parte más interesante de la difracción: su utilidad. La interferencia depende de cómo choca la luz con un objeto, es decir, es sensible a la estructura del objeto.

Una de las principales utilidades de la difracción es el estudio de la estructura atómica de un material, en particular si es cristalino. En la física de materiales, un cristal no es un vidrio como el de la ventana, o del botellín de cerveza, sino un material cuyos átomos se alinean formando planos, como es el cristal de la sal de cocina, el diamante, o el grafito por ejemplo. Todos están formados por planos que contienen átomos colocados de forma regular (es decir, repitiendo un patrón), con la diferencia de cómo están colocados estos planos, y los átomos en ellos.

Si ahora iluminamos el cristal con un haz de Rayos - X a estos cristales, la luz se re-emitirá desde los átomos de cada uno de estos planos, que están separados por una distancia d:

La interferencia de estos Rayos - X re-emitidos produce un patrón de interferencia que es característico de la estructura (la distancia entre planos d), y también de cómo están colocados éstos átomos en cada plano. Observando los picos de mayor intensidad, en qué dirección han salido, y en qué dirección venía el haz, es posible determinar la estructura del material.

Difracción y piramidiotas

Aquel que lea habitualmente la lista de correos libre y sin censura Charlatanes, estará al corriente de quién es nuestro piramidólogo favorito, y que su jefe o gurú dice haber descubierto la estructura cristalina del agua, que (oh, casualidades de la vida) es la de una pirámide, donde en cada uno de sus cinco vértices hay colocada un "monómero" (sic) de agua, desafiando no ya las leyes de la física y química, y los experimentos de difracción de rayos X que demuestran que el agua sólida (hielo) cristaliza con estructura hexagonal, sino también las matemáticas y geometría básicas.

La razón es simple: un cristal rellena todo el espacio disponible repitiendo periódicamente una misma estructura, sin dejar huecos vacíos. Empieza por pensar en dos dimensiones: Se puede rellenar un papel dibujando cuadrados, paralelogramos, o hexágonos como en las colmenas de abejas, sin dejar ningún hueco libre. En cambio, si lo intentas con un pentágono, lo más que puedes conseguir es algo así:

donde la zona pintada de azul es un hueco vacío no rellenado por los pentágonos. Si piensas ahora en 3 dimensiones, puedes llenar un volumen con cubos o paralelepípedos, con todos sus lados compartidos con el siguiente cubo o paralelepípedo. Pero con una pirámide ocurre lo mismo que con los pentágonos: es imposible llenar todo un volumen sin dejar huecos vacíos entre algunas paredes. Haz la prueba.

(Sin duda, alguien más experto en matemáticas será capaz de explicarlo mejor y con más rigor)

La razón que prohibe la estructura cristalina piramidal del agua no es física o química, sino matemática. Pero en todo caso, nada más fácil que un experimento de difracción de Rayos - X para comprobar si la estructura piramidal del agua que sugiere el sujeto éste es o no incorrecta. ¿Lo veremos algún día?

Malas vibraciones

El origen de las vibraciones

Anteriormente establecimos una hipótesis acerca de cómo una vibración del cabezal de escritura podría afectar en una grabación. Como toda hipótesis que pretenda ser válida, debe basarse en una realidad que sea posible comprobar, y determinar si es lo suficientemente realista (aunque tenga aproximaciones o simplificaciones), o si hace falta modificarla en algún punto.

Supusimos que las oscilaciones del cabezal eran tales que se acercaba y alejaba de la cinta magnética, de forma que modulaba la amplitud del ruido, lo cual describían estas ecuaciones:

Donde r0 es la distancia en condiciones normales y r la distancia cuando vibra el cabezal. ¿Se acerca esto a la realidad?

Veamos los cabezales de un radiocassette:

Al pulsar la tecla de grabar, bajan los dos cabezales, y una rueda de goma. La rueda gira para tensar y arrastrar la cinta. Los cabezales por su parte llegan a hacer contacto con la cinta, y la empujan. En el caso del cabezal de escritura, la cinta queda además atrapada entre él, y un fleje (o muelle) que tiene la propia cinta. Este fleje ejerce una fuerza hacia el cabezal, de forma que aprisiona la cinta, y los pone en buen contacto.

Cuando hay vibraciones que desplacen ligeramente el cabezal de arriba a abajo, el fleje absorbe esa vibración y mantiene el contacto entre ambos.

Al tacto, el fleje no es un muelle "duro", sino que se desplaza con facilidad. Con una vibración fuerte, o un golpe seco, el fleje podría "rebotar" demasiado, rompiendo el buen contacto, y separando la cinta del cabezal. Más aún, la rueda tensora baja y sube a la vez que el cabezal, por lo que un golpe o vibración fuerte podría hacer que se desplazara ligeramente y dejar de tensar brevemente la cinta. Esto también dificultaría el buen contacto entre cinta y cabezal.

Notar que el cabezal de borrado no tiene un fleje o muelle que absorba o minimice las vibraciones, por lo que el borrado podría no ser correcto en una de estas vibraciones, y dejar rastro de grabaciones anteriores. Es una posibilidad que no vamos a tener en cuenta en lo que sigue.

Para una descripción más real de las vibraciones hay que tener en cuenta que la cinta ya está en contacto con el cabezal, y por tanto, no va a estar más cerca del valor nominal r₀.

Aclaración: "en contacto", no quiere decir que r₀=0. La cinta es una lámina de plástico, con varios recubrimientos, y entre el material magnético y el cabezal hay una capa protectora, para evitar que se raye o deteriore. Igualmente, como "distancia cero" se toma el centro del entrehierro del cabezal donde se surge el campo magnético, y la cinta va a pasar por debajo del entrehierro:

Esto quiere decir (para quien lo quiera calcular), que si la oscilación hace que r sea menor que r₀, entonces se debe tomar el valor r0. En la siguiente gráfica, la línea negra representa el valor de r(t), mientras que la roja es la variación del campo magnético que produciría: al alejarse el cabezal, disminuiría el campo, y por tanto el valor de la magnetización que quedaría en la cinta:

¿Qué valores se pueden poner para simular sonidos? Para empezar, el valor de r₀ es indiferente. El hecho de definir la amplitud A como se hizo, permite que la cantidad [r₀/r(t)] sea independiente de r₀.

Los otros valores son libres para experimentar aquel que quiera. La frecuencia determina el tono del click. La constante de tiempo t₀ está relacionado con el tiempo que tarda en desaparecer el sonido. Cuanto menor sea, menos tiempo tardarán en desaparecer las oscilaciones, y más apariencia de golpe tiene el sonido

Si alguien quiere probar a simular, las instrucciones son estas:

- Generar un ruido marrón con una intensidad arbitraria: Escoger un valor arbitrario de la magnetización M₀, de la amplitud A (A=1 es suficiente), de la frecuencia f, de t₀ y un valor inicial de la fase (fi) de la intensidad. Calcular un número aleatorio entre 0 y 1. Si es mayor de 0.5, sumar a la fase un valor determinado. Si es menor, restarlo.
- Calcular la oscilación del cabezal y la cantidad [r₀/r(t)]. Si es mayor de 1, entonces igualarlo a 1.
- Calcular el valor final como M₀·cos(fi)·[r₀/r(t)]

¿Es este modelo realista?

Hay que reconocer que las cintas vienen bien preparadas para soportar vibraciones, pero sólo hasta un límite. Si hay golpes, o vibraciones fuertes, ya sea por llevar la grabadora en la mano, o colgada del cuello[1], si está por un suelo que transmite bien vibraciones mientras la gente pasea a su alrededor sin prestar atención[2], o se cae un objeto al suelo, no es imposible que pudiera suceder.

Hay que tener en cuenta que las oscilaciones tienen una amplitud del orden de r₀. Y esta distancia, aunque no es cero, es muy pequeña (menos de 0.1 milímetros, por poner un valor). Cuanto más pequeña, más facilidad hay de que en algún momento la cinta se pueda separar hasta por ejemplo r=2r₀ (que serían 0.2 milímetros)

Hemos supuesto una vibración simple, de una sola frecuencia. En un modelo más real, esta vibración podría ser cualquier función que cumpliera dos requisitos:
- Que se amortigüe con el tiempo (recupera el valor previo a la perturbación)
- Que sea periódica. Siendo así, se puede expresar como una suma de senos y/o cosenos de distintas frecuencias.

Se podría escribir algo así

Es decir, la oscilación como un conjunto de frecuencias, que no tendrían por qué ser armónicas entre ellas, ni estar relacionadas, y que dependería del aparato de grabación (cómo transmite las vibraciones su carcasa y mecanismo que sujeta los cabezales) y del fleje de la cinta. Para la misma cinta y aparato, el click debería ser siempre igual.

Por hacer una prueba, he aquí un click generado con 3 frecuencias distintas arbitrarias. Suena más real que un click de una sola frecuencia (500hz).

Y para comparar, el click de verdad

Vibraciones en el micrófono

Hay que reconocer que la vibración del cabezal es un tanto complicada. Las cintas, y el sistema entero está diseñado para absorberlas, así que sólo parecen posibles vibraciones fuertes, debidas a un golpe o movimientos bruscos.

Ya hemos mencionado alguna vez que emplear un poco de método y rigor hace posible estudiar cualquier hipótesis y encontrar resultados con los que saber las posibilidades reales de que una hipótesis así no sea errónea. En este caso, si bien las vibraciones no son imposibles, si parecen un poco difíciles de ocurrir.

Vamos buscar otra hipótesis más probable, modificándo ésta ligeramente. Mantenemos la idea básica de una oscilación amortiguada, pero en vez de suponer que ocurren en el cabezal, vamos a suponer que es en el micrófono.

Los micrófonos más extendidos (y usados por expertos en psicofonías), son del tipo dinámico. Están basados en una membrana, a la que está pegada una barra ferromagnética rodeada de una bobina de cable. A una corta distancia se coloca un imán potente. Cuando llega un sonido, la membrana desplaza la barra metálica. Al estar dentro del campo magnético del imán, la vibración produce una señal eléctrica en la bobina, que es la que se recoge en un amplificador para ser grabada. El funcionamiento es exactamente el inverso a un auricular o altavoz. Incluso un pequeño auricular puede servir de micrófono. Es una aplicación directa de la Ley de Faraday (nada que ver con las jaulas), una de las cuatro ecuaciones de Maxwell que explican el electromagnetismo, y por las que se rigen las grabadoras y micrófonos.

Pincha aquí para ver un ejemplo de cómo funciona un altavoz. El micrófono funcionaría de forma inversa.

Al contrario que en el cassette, que procuraba mantener la cinta magnética en contacto con el cabezal, en un micrófono (o altavoz) lo que interesa es que se pueda mover y vibrar fácilmente con el sonido, para convertir ese movimiento en electricidad. Esto hace que sea más sensible a vibraciones y golpes que el cabezal.

Puesto en ecuaciones, recordamos que la magnetización en una cinta dependía de dos factores: la distancia al cabezal (que ahora suponemos constante) y la intensidad eléctrica, que ahora no va a modular el ruido, sino que es una señal que se va a añadir a éste:

donde A es otra vez la amplitud de las vibraciones, definida de esta forma:
Si A=1, la oscilación produce una intensidad que varía entre I=-I₀ hasta I=I₀
Si A=2, la oscilación de la intensidad va desde I=-2I₀ hasta I=2·I₀ . (Que I sea negativo no representa ningún problema)

De esta forma, el cálculo es independiente del valor de I₀

Al igual que antes, el modelo se puede hacer más real suponiendo que la oscilación no ocurre a una sola frecuencia, sino que puede ser una función arbitraria, con mezcla de varias frecuencias.

Click de una sola frecuencia (f=500 hz, t0=0.05).
Click con tres frecuencias.

Juntando sonidos

Hay una gran diferencia entre las dos formas de generar el sonido. Si suponemos que el sonido se genera por una vibración del cabezal, el sonido aparece como una modulación del ruido de fondo, el cual incluiría el ruido del motor. En realidad, es una atenuación del ruido de fondo, excepto de las frecuencias que generan la vibración.

Si suponemos una vibración del micrófono, entonces tenemos un ruido que se suma sin alterar el resto de sonidos ya presentes, se añaden nuevas frecuencias.

He aquí dos ejemplos en los que se ha añadido una frecuencia simulando un ruido de motor a 200 hz:

Click del cabezal
Click del micrófono


Bricomanía: un micrófono casero

He aquí la forma de hacerse un "micrófono" casero: Busca un hierro o material ferromagnético, como un destornillador. Enrolla un cable, y conecta los extremos a una clavija conectada a la tarjeta de sonido:

Ahora busca un imán potente, como el de un altavoz viejo, y acércalos. Colócalos de tal manera que la bobina pueda vibrar. Por ejemplo, aquí la he puesto sobre un soporte metálico hueco:

que golpeado suena tal que así: click

Dependiendo donde se coloque (y cómo), el sonido será de una forma u otra. Por ejemplo, sobre un vaso:

que al golpearlo suena de esta otra forma: click

Las frecuencias o sonidos que puede registrar un dispositivo (o apaño) como éstos depende de las propiedades elásticas de cada material; es decir, dependen de cómo vibran, y cada objeto y material tiene sus vibraciones características, también llamadas resonancias. La barra o el vaso son muy rígidos, y vibran poco, comparados con un micrófono real, donde la membrana está diseñada para tal fin, y permite registrar un amplio rango de frecuencias, que viene siempre documentado en un gráfico que muestra la intensidad relativa con que registra de cada frecuencia

Espectro de un micrófono dinámico Sennheiser 825-s

Si hay un golpe en la carcasa del micrófono, éste se transmite a la membrana, de igual forma que se transmiten las vibraciones desde un vaso a la punta del destornillador, y puede quedar registrado.

Resumiendo

En cualquier sistema siempre hay elementos que son susceptibles de vibrar, y que en algunos casos pueden influir en una señal eléctrica o magnética, y en cómo se registran estas señales. Prueba de ello son las medidas de seguridad que se toman en una cinta, por ejemplo, para minimizar estas vibraciones.

Nota: El click "de verdad" está cogido de la sección de psicofonías de Adimensional (click_metalico.mp3). En el sonido completo se aprecia como después del click, aumenta el nivel de ruido, como si se hubiera cogido la grabadora para subir el volumen en mitad de la grabación.

[1] http://www.aaevp.com/articles/articles_about_evp1.htm

"At one point I discovered, to my joy, that if I hung my recorder around my neck and walked around my flat as I was recording, the EVP utterances became magnified and much more abundant."

Tina Laurent, Asociación Americana del Fenómeno de Voces Electrónicas

[2] http://jabber-hispano.org/mesias/chat/seip/fomalhaut1.htm

"Por protocolo y por lo que pudiese registrarse, dejamos un grabador en marcha, a la cual no prestamos mucha anteción durante nuestra breve estancia (...)
No sólo los registros psicofónicos fueron desmesurados, sino que también fueron contundentes, objetivos y dennotaban cierta proximidad hacia nosotros, algo que nos sobrecogió y que de la misma forma hizo cuestionarnos numerosas preguntas;
¿Por qué esa noche, cuando apenas teníamos controlado el medio?"

David Ruiz, investigador de psicofonías

Click!

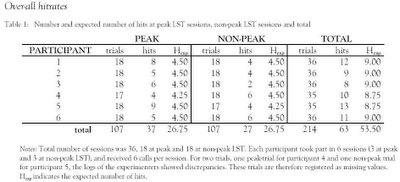
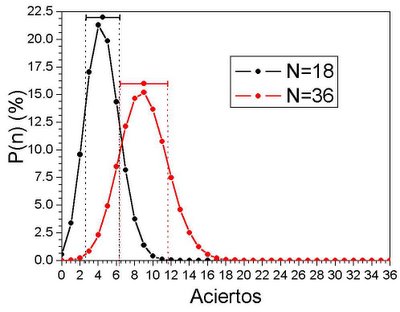
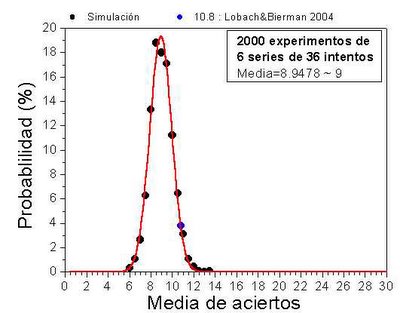
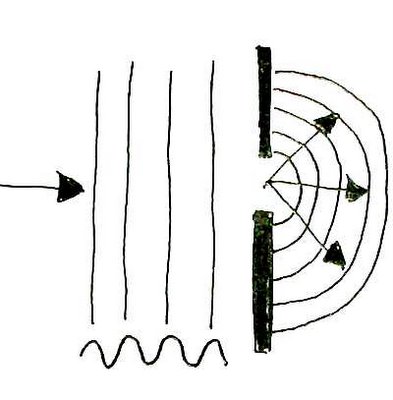
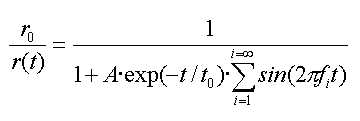Hay que ver lo que dan de sí las psicofonías.

En anteriores entradas estuvimos viendo qué tipo de ruido eléctrico y electromagnético puede haber en una grabadora, y cómo estos ruidos podían estar a su vez presentes en los sonidos que identificaban a las supuestas psicofonías. También vimos cómo una jaula de Faraday no es un elemento mágico, sino que tiene sus limitaciones y puede dejar pasar radiación externa, por muy perfecta que se construya. Ahora vamos a tratar otro tipo de ruido, en concreto qué tipo de ruido o "huella" puede dejar una vibración del cabezal de grabación.

Para ello vamos primeramente a conocer cuál es la física en la que se basa el proceso de grabación de una cinta, que siempre es interesante saberlo.

Magnetismo

Todos sabemos que la materia está compuesta de átomos. Éstos átomos, en su forma más simple, se pueden entender como un núcleo central con carga positiva alrededor del cual giran electrones con carga negativa. Este giro es por definición una corriente eléctrica, que a su vez genera un campo magnético. Así, cuando se habla de magnetismo, la forma más simple de imaginar la materia es como compuesta por una multitud de pequeños imanes llamados dipolos magnéticos, que se caracterizan por tener un valor (momento dipolar, u) y una orientación, o sentido en que el campo magnético atraviesa el átomo:

En un material sólido, todos estos dipolos tomados en conjunto se describen por una propiedad llamada "magnetización", que llamaremos M, que describe el valor y orientación promedio de todos los dipolos. Si el material tiene una densidad N (átomos/m³), entonces, M=N[u], donde [u] es el promedio de todos los dipolos considerados. En ausencia de un campo magnético (que llamaremos H), todos estos dipolos están orientados al azar, de forma que en promedio, los campos creados por cada uno se cancelan mutuamente, y entonces [u]=0 y M=0.

Cuando se aplica un H externo, el valor u cambia su valor u orientación de forma que que tomado en promedio este cambio propicia la aparición de una magnetización neta. La respuesta depende del tipo de material.

Tenemos primeramente materiales diamagnéticos: al aplicar un H, éste afecta a la velocidad de giro de los electrones, de forma que todos los dipolos cambian su valor,(pero no su orientación) para oponerse al campo H que le está afectando: Se consigue una magnetización neta negativa, que crea un campo magnético en sentido contrario a H. Si el dipolo está originalmente alineado en la dirección del campo, entonces su momento dipolar se reduce, y si está en sentido contrario, entonces aumenta.

En segundo lugar, tenemos materiales paramagnéticos: además del cambio en el giro de los electrones, los dipolos se reorientan para colocarse alineados con el campo H, de forma que ahora al tomar el promedio de los momentos dipolares no se cancelan, sino que se refuerzan, apareciendo una magnetización positiva (crean un campo en el mismo sentido que H).

En estos dos tipos materiales, M desaparece cuando se elimina H. Pero tenemos un tercer tipo de materiales, que son los que nos interesan de verdad, los ferromagnéticos: Se comportan como los paramagnéticos, pero son capaces de mantener la magnetización cuando se elimina el campo magnético que la crea. Si no existieran estos materiales, no existirían los imanes permanentes, ni motores de grabadoras, ni las cintas de cassette donde grabar psicofonías.

En estos materiales, unos pocos dipolos crean un campo tan fuerte que son capaces de hacer orientarse a los que tienen en su entorno más cercano. De esta forma, el material se divide en muchas zonas, más o menos grandes llamadas dominios, con una magnetización neta, pero con distinta orientación, de forma que tomado en su conjunto, el material puede tener una magnetización nula. Al aplicar un campo externo, algunos de estos dominios se reorientan para alinearse con H, creando una M positiva. Cuando se quita el campo, permanecen con esa orientación, y el material mantiene una magnetización total distinta de cero.

Esta figura representa la curva típica de un material ferromagnético. Representa el valor de M en función de H

Si partimos del punto a de la gráfica, es decir, cuando M=0, y aplicamos un campo magnético externo pequeño, algunos dominios se reorientan creando una magnetización, que se mantiene al retirar H. El valor de M aumenta con H, hasta que llega al punto b, donde todos los dominios estarían totalmente orientados, y alcanzaríamos un valor de saturación, que no se puede superar porque no quedan dominios o dipolos que orientar. Al eliminar H, siempre hay un pequeño descenso del valor de saturación de M debido a que por temperatura, algunos dipolos pueden desorientarse, quedando un valor de la magnetización de saturación cuando H=0, que se llama magnetización remanente, Mr (punto c)

Si ahora aplicamos un campo H en sentido contrario, la magnetización se reduce poco durante un pequeño intervalo, hasta que el campo es lo suficientemente intenso como para comenzar a reorientar los dominios. En esta reorientación, hay un punto (punto d) para el cual se puede anular M, es decir, tenemos tantos dipolos orientados en un sentido, como en el contrario, y por tanto el promedio es cero. El valor de este campo Hc, es llamado campo cohercitivo. Si se aumenta más la intensidad del campo, los dominios se siguen reorientando hasta alcanzar de nuevo la saturación, pero esta vez en sentido opuesto (punto e). Este tipo de curva es típica de materiales ferromagnéticos, y se llaman curvas de histéresis, que son importantes dependiendo del uso que se le de al material.

Cintas de cassette

Una cinta de cassette es un material ferromagnético, que se magnetiza para "recordar" la información. Un sonido se convierte en electricidad. Esta corriente eléctrica se convierte en un campo magnético, y éste en un valor de magnetización sobre la cinta. A la hora de reproducir, la magnetización crea un campo magnético, que genera una corriente eléctrica que es transformada en sonido.

Un cabezal de grabación es como en la figura: una espira, enrrollada en un hierro que tiene un hueco en el otro extremo.

La corriente por la espira crea un campo magnético que es guiado por el hierro. Al llegar al hueco, el campo magnético sale de éste, creando un campo no solo en el hueco, sino también alrededor. Este campo de alrededor es el que magnetiza la cinta. La magnetización producida depende de la intensidad del campo magnético, que a su vez depende de la intensidad de la corriente eléctrica de la espira.

La cinta se divide en pequeñas zonas con dominios que mantienen la magnetización. Al grabar, a cinta pasa primero por un cabezal de borrado, que provoca una magnetización de saturación en cada uno, pero con una orientación aleatoria, de forma que sólo se obtiene ruido sin información. Al tener cada zona una magnetización previa, no se puede grabar directamente la señal, ya que el resultado final depende del estado inicial.

Dependiendo del valor obtenido en el borrado, al aplicar un campo con el valor marcado por la línea de puntos, se podría obtener una magnetización final en el grabado entre C y D. Como esto no es aceptable, en el grabado se añade una señal alterna de alta frecuencia (referida como bias) que recorre el ciclo entero de la histéresis, y hace que en promedio la magnetización sea nula. De esta forma, cuando no hay señal a grabar, la magnetización final es cero. Si hay señal, entonces el valor promedio se desplaza hasta una magnetización proporcional a ésta.

Más información sobre el grabado de cintas, aquí.

Vibración del cabezal

La magnetización de la cinta depende de la intensidad de campo magnético que llega a la superficie de la cinta, y que es proporcional a la señal que se quiere grabar. Las condiciones de trabajo son además tales que hay linearidad entre M y H: es decir, si se aumenta al doble H, entonces M también aumenta el doble (siempre que no superemos el valor de saturación). Además, el campo magnético creado por una espira es proporcional a la intensidad que va por ella, así que al final, la magnetización será directamente proporcional a la corriente I que va por la espira del cabezal.

La intensidad de campo magnético depende no solo de la intensidad de la corriente, sino también de la distancia entre el cabezal de grabado y la cinta (r). A mayor corriente, mayor campo, pero a mayor distancia, menor intensidad. Se puede escribir la dependencia de M con I y r:

(donde k es una constante. Supondremos 1/r porque es el caso "más favorable": la disminución de M es más lenta que si fuera 1/r², 1/r³, o cualquier otra potencia mayor que 1)

Para grabar una señal dependiente del tiempo, M debe variar entre dominio y dominio de la cinta, lo cual se hace normalmente a través de I. Si solo se está grabando ruido, la intensidad se puede escribir de esta forma:

donde I₀ es la amplitud del ruido, y fi(t) es una fase aleatoria. Si el cabezal se mantiene a una distancia r₀ constante de la cinta, la magnetización que queda grabada es simplemente un ruido de amplitud constante kI₀/r₀:

¿Qué ocurre al desplazar el cabezal, por una vibración o un golpe?

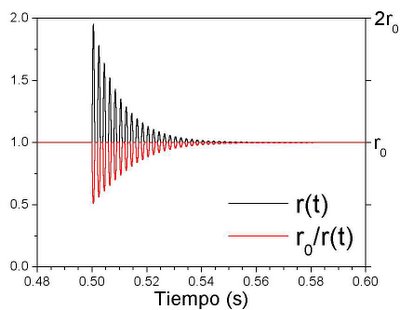
Si suponemos un desplazamiento muy pequeño, y que además éste tiende a recuperar su posición inicial a una distancia r₀ de la cinta, r(t) se puede describir de la forma más sencilla así:

Representa una oscilación de frecuencia f₀ en torno al valor r₀ que se va apagando con una constante de tiempo característico t₀, hasta recuperar el valor constante normal. A es la amplitud del la oscilación, entendida de esta forma:

Si A=1, entonces la oscilación tiene una amplitud r₀, y r(t) varía entre 0 y 2r₀.
Si A=2, entonces la oscilación tiene una amplitud 2r₀, y r(t) varía entre -r₀ y 3r₀

Y así sucesivamente... Un valor menor que cero no tiene sentido. Cuando r=0, hay que suponer que el cabezal empuja la cinta, y se la lleva con él manteniendo la distancia constante, hasta que vuelve a rebotar hacia arriba.

¿Qué valor puede tener r₀, la distancia entre cabezal y cinta? Muy pequeña. Por hacernos una idea, pongamos que medio milímetro (que posiblemente sea demasiado). Con A=1, la distancia del cabezal oscilaría entre 0 y 1 milímetros. Si r₀=0.1 mm, entonces oscilaría entre 0 y 0.2 mm

Ahora la magnetización se puede escribir de esta forma:

Si a partir de la primera ecuación, multiplicamos y dividimos por r₀, y reagrupamos los términos, nos queda la magnetización original sin vibración, que tiene una amplitud M₀, pero modulada por la cantidad r₀/r(t). Esto es interesante: la vibración es un ruido que no se añade (se suma) al ya existente, sino que lo modula, hace variar la amplitud del ruido original.

Imaginemos que se está grabando una señal de ruido constante, y al coger la grabadora, o por una vibración que se transmite por el suelo, el cabezal sufre una vibración, que se amortigua y desaparece en menos de medio segundo. La magnetización sufrirá esta modulación, aunque la corriente sea constante. Pero al reproducir la cinta, si el cabezal mantiene una posición fija, la modulación del ruido producirá un cambio en la intensidad eléctrica, se interpretará como tal, y será convertida a sonido en los altavoces: la vibración se interpretará al reproducir como si se hubiera grabado un sonido.

¡Click! Probando un dos tres... ¿Se me oye?

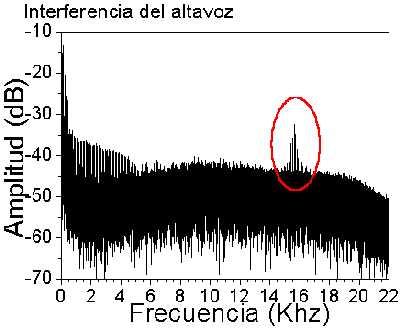
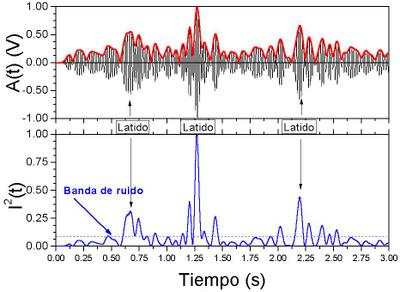
Por no ser muy pesados, en una segunda parte veremos que al simular estas vibraciones aparece este sonido:

Click

Que recuerda bastante a los clicks que se escuchan en algunas psicofonías, y que los entendidos del tema dicen que es habitual que aparezcan justo antes de oírse una psicofonía de las de verdad.

No cambien de canal.

El mito de la jaula de Faraday

Existen palabras mágicas que de pronto parecen explicar todo, como "Mecánica Cuántica" (con mayúscula, que si no, pierden sus poderes). Y como no podía ser de otra manera, también existen artilugios mágicos que de pronto hacen que toda explicación racional pueda ser deshechada, de una forma que incluso se podría llamar dogmática. Es el caso de las Jaulas de Faraday (con mayúscula, claro) cuando el tema de discusión son las psicofonías. Sólo el hecho de incluir una de éstas hace imposible la existencia de interferencias externas, y por tanto cualquier cosa que se oiga en una grabación es automáticamente paranormal.

En un mundo ideal tal vez pueda ser así, que una jaula de Faraday sea capaz de eliminar cualquier interferencia electromagnética, y proteger el circuito en su interior. Sin embargo, el mundo real siempre es un poco diferente, dejando los mundos ideales como meras aproximaciones que en algunos casos pueden ser válidas, pero que en otros no lo son tanto.

Así pues, en los laboratorios secretos de Gluon con Leche, hemos construido una pequeña jaula de Faraday. Cogiendo un tetra-brik, para aprovechar la forma de caja, lo hemos envuelto con tres capas de papel de aluminio, del que todos tenemos en la cocina, y le hemos añadido una tapa de cartón, también envuelta en aluminio, y ha quedado así de bonita.

Sí, es casera, pero no por ello menos efectiva, como se verá más adelante.

Atenuación de las ondas

La física detrás de una jaula de Faraday está en las propiedades de las ondas electromagnéticas cuando se propagan en un medio conductor, como es el aluminio. En un material conductor, lo átomos que lo forman se enlazan de forma que comparten sus electrones de los orbitales más externos, y son libres de moverse por todo el material. Sin embargo, esta alta densidad de electrones libres hace que cuando una onda electromagnética intenta desplazarse por un medio así, se atenúe. Este es un matiz importante: la onda se atenúa, pero no desaparece.

Cada material posee una profundidad característica de atenuación que determina la distancia que recorre una onda hasta que su campo eléctrico se reduce en un factor 1/e=0.367 (siendo e=2.71828182845904...), es decir, cuando el campo eléctrico se reduce en un 36.7%. Nos interesa más la densidad de potencia (o cantidad de energía que atraviesa un área determinada por segundo) de una onda electromagnética, que viene dada por el cuadrado del campo eléctrico, así que en esa misma distancia, la potencia de la onda disminuye en un factor 1/e²=0.135, un 13.5%

Un 13.5% puede ser una cantidad pequeña, pero no es nula. La jaula de Faraday juega con el espesor de la paredes para que la atenuación sea la necesaria como para que la potencia que consigue atravesarla sea despeciable. Cuanto mayor sea el espesor, menos energía traspasará la jaula e interferirá con el circuito.

La profundidad característica depende además de la frecuencia de la onda incidente, de forma que una jaula puede ser efectiva para unas frecuencias, pero mala para otras. En general, cuanto mayor es la frecuencia, menor es la profundidad característica (se atenúa más rápido). He aquí una gráfica para varios conductores:

Para el aluminio, una frecuencia de 60hz necesita una pared con un espesor de alrededor de 1 cm para ser atenuada un 13%. Sin embargo, para 3 Ghz, se consigue la misma atenuación con menos de 2 micras (0.002 milímetros). De los materiales mostrados, el hierro sería el mejor de todos para hacer una jaula de Faraday, porque para el mismo espesor, atenúa más la señal que los otros materiales.

El papel de aluminio es realmente finito, aunque se le den tres vueltas. Pero para probar que nuestra jaula casera puede ejercer su función, hemos hecho lo siguiente:

Primero, hemos colocado el walkman de otras veces a unos 10 cm de un móvil, y hemos llamado. Luego hemos metido el walkman en la jaula casera, con el móvil a la misma distancia, y hemos vuelto a llamar:

Aunque no se vean en el gráfico, las interferencias también se oyen en el segundo caso, a pesar de estar atenuadas por tener que atravesar el aluminio. La frecuencia de funcionamiento de un móvil suele estar en torno a las microondas (~ 1.8 Ghz), una frecuencia que es fácilmente atenuada por el aluminio (con 5 micras de espesor, sólo pasaría un 1% de la potencia de una onda de 3 Ghz). Tres vueltas de papel de aluminio es poco, pero es probable que sean más de 5 micras. Y aún así es capaz de generar interferencias.

Hay que tener en cuenta la densidad de potencia de la onda original. Un 1% podría ser suficiente para generar interferencias. Eso sin contar con imperfecciones de la propia jaula, agujeros para pasar cables, poner botones de plástico, ventanas..., por donde se colaría parte de radiación.

Se puede llegar a una situación en que la cantidad de radiación que traspasa una jaula de Faraday es tan ínfima que se puede despreciar frente a las señales con que se va a trabajar. En otros casos, puede que no. Lo que no se puede hacer es creer de primeras que sólo por el hecho de colocar la jaula se eliminan las todas interferencias, sino que hay que comprobarlo.

Capacidades residuales

A la vista de estos espectros, ¿quién sabría decir cual fue hecho sin jaula de Faraday?

No. Esa se hizo con jaula.



Sólo la c) fue hecha sin jaula de Faraday. La a) y b) fueron hechas con la jaula, aunque con una pequeña diferencia entre ambas, que comentaremos más adelante.

Lo primero que llama la atención es cómo es posible que usando una jaula, se obtenga un resultado peor que sin usarla. Si no funcionara, lo lógico sería tener un espectro como el c), pero no que de pronto aparezcan contribuciones no esperadas.

Hay que tener en cuenta lo siguiente: tenemos un circuito, lleno de dispositivos conectados por materiales conductores, rodeado por otro conductor (la jaula), y un espacio entre medias relleno de aire, que es una material dieléctrico: eso es un condensador

El circuito tiene su propia fuente de voltaje (las pilas) y forma un circuito cerrado, mientras que la jaula no tiene referencia alguna de voltaje respecto del circuito, y con cada elemento conductor de éste va a formar un condensador. Al no tener referencia, el potencial de la jaula varía libremente, es un ruido aleatorio, que se transmite a través de estos condensadores. La capacidad e influencia que tengan depende de la geometría. Si en vez de una fluctuación aleatoria, el potencial está forzado por una interferencia externa, ésta señal se puede transmitir al circuito.

Si a alguien le da por destripar algún aparato, como el ordenador por ejemplo, en muchos de ellos encontrará una carcasa metálica, una jaula de Faraday. Y además, esta carcasa está conectada a tierra, es decir, está conectada al propio circuito del aparato en un punto concreto de referencia, de forma que mantiene un potencial definido y constante (generalmente definido como V=0) conocido respecto a cualquier otro punto del circuito. No es una solución definitiva al problema de capacidades residuales, pero sí la minimiza en gran medida.

Esto es justamente lo que falta en nuestra jaula de Faraday. Así que hemos conectado un cable al polo negativo de las pilas del walkman y el otro extremo se ha colocado haciendo contacto con el aluminio de la jaula, y entonces han desaparecido los picos de alta frecuencia, como se ve en el espectro a).

Además, hemos medido la relación señal/ruido de las frecuencias de 50hz y 150 hz:

Se han medido sin jaula, con jaula, y con la jaula conectada a tierra (al polo - de las pilas), 5 espectros de cada una para hacer la media. A 50 Hz, las barras de error son grandes y se solapan, así que no se puede asegurar que haya influencia alguna. A 150 hz sin embargo, se ve como al poner la jaula, hay una pequeña reducción de la relación señal/ruido, aunque todavía se solapan ligeramente los errores, pero cuando se conecta a tierra la relación señal/ruido cae de 13-17 a 6, es decir, la interferencia creada a 150 hz disminuye para acercarse más al nivel de ruido, y en principio, se podría pensar que es debido a minimizar el efecto de las capacidades parásitas.

Se puede ver también que la barra de error es menor siempre en el caso de la jaula conectada a tierra, lo que da idea también de mayor estabilidad en las interferencias que se crean.

Qué bonito sería el mundo y qué fácil sería todo si vivieramos en un mundo ideal. Pero no es así. El mundo ideal es la primera aproximación a la realidad, y en muchas ocasiones, es una aproximación válida. Sin embargo, es necesario saber hasta donde llega la validez de la aproximación, si nuestros instrumentos funcionan dentro de los límites de la aproximación, y qué otros fenómenos pueden darse lugar, para que cuando ocurran cosas inesperadas saber por qué han salido.

Ruidos del Más Allá II

En el capítulo anterior...

Vimos qué tipo de ruido puede tener un aparato como una grabadora. Es un ruido intrínseco al propio aparato, es decir, es imposible deshacerse de él, y siempre va a estar presente, en mayor o menor medida. Por eso conocer la fuente que lo origina, y las propiedades que lo caracterizan es fundamental para quien quiera grabar supuestas voces psicofónicas, y querer distinguir lo que es sólo ruido, lo que son variaciones del ruido natural del aparato, y lo que son señales distintas a éstas.

La principal fuente de ruido vimos que era el motor. Introduce una intensidad eléctrica con una cierta frecuencia que pasada por un altavoz, genera sonido en el rango audible. Una variación, o perturbación en su giro puede producir cambios en esa frecuencia. Por otro lado, vimos que radiaciones externas también pueden añadirse al ruido, donde la más importante es la producida por la red eléctrica de 50 hz y los armónicos que introduce dentro del circuito eléctrico. En general, cualquier aparato puede producir una radiación con una frecuencia característica suya: vimos el ejemplo de un monitor donde se colaba la frecuencia de barrido vertical, y cómo la corriente eléctrica de unos auriculares conectados a un radio cassette interfería con el circuito del walkman para registrar la "Marcha Radetzky", lo cual salvando las distancias, y el tema de la modulación de la señal, llevaría a la pregunta de si una señal de radio (no solo la comercial, sino también radioaficionados, o incluso satélites de comunicación: la radiofrecuencia va desde los hz hasta los Ghz) puede colarse igualmente en un grabador, aún no registrando sonido inteligible, pero sí introduciendo algún tipo de sonido que entre tanto ruido pueda interpretarse como palabras o música. O si incluso fuese posible que la señal fuera demodulada (el circuito que lo hace es muy simple), y registrar sonidos inteligibles. La pregunta tiene bastante sentido, a la vista de los resultados anteriores.

También conviene recordar que éste tipo de ruido es sólo una de las varias contribuciones que se pueden tener: la cinta tiene su propio ruido, el micrófono tiene sus características de frecuencia y ganancia. Incluso el lugar donde se esté grabando puede presentar ruidos, porque a cierta distancia haya fuentes de ruido, que aunque atenuadas lleguen a poder registrarse (en especial los sonidos graves), corrientes de viento, edificios que "crujen", tendidos de alta tensión, vibraciones del suelo, cercanía a una carretera, pájaros, goteras, paseantes no esperados gritando en la lejanía... El ruido final va a ser un conjunto de muchos factores, y quien quiera ponerse a intentar registrar psicofonías va a tener que caracterizar primero todos y cada uno de ellos para estar completamente seguro de estar grabando "otra cosa" distinta al ruido, sonidos del ambiente, o interferencias de cualquier tipo.

Una de psicofonías

Es obvio que nadie que quiera evitar interferencias va a enrollar su grabadora con un cable por donde pasa una corriente eléctrica dependiente del tiempo, ni manipulará el motor para que su movimiento de giro no sea uniforme. Así que la pregunta del millón es ¿estos ruidos, tanto el intrínseco a la grabadora como el producido por compatibilidad electromagnética, pueden llegar a confundirse con una psicofonía?

Quizás por la falta de entrenamiento en el oído (algo que los expertos reconocen como muy importante), no hemos detectado nada que nos parezca algo en todas las pruebas que hemos hecho. Así que hemos buscado por varias webs alguna psicofonía "de las de verdad" para comprobarlo.

Hay que decir que es difícil encontrar un psicofonía que no haya sido previamente tratada, sino que la mayoría se hallan ya "analizadas", si por ello entendemos "pasarle todos los filtros y ecualizados posibles hasta que suene algo más claro". Si no se conocen los ruidos característicos del sistema entero (grabadora, micrófono, cinta, ambiente, ...) se corre el riesgo de perder información. Incluso el formato de grabación si incluye compresión (como el MP3) elimina información. Puede o no ser relevante, pero siempre es mejor tratar los datos "crudos".

Cada aparato y situación es un mundo, y es tarea del interesado determinar cual es el ruido en cada caso. Intentar analizar independientemente un supuesto sonido sin conocer el aparato, ni las circunstancias en que se grabó no es algo trivial de hacer, y puede ser fácil meter la pata. Así, no es intención nuestra dar una explicación definitiva sobre el origen de las dos psicofonías que hemos seleccionado, sino sólo hacer notar cómo éstas poseen características que se pueden relacionar con lo explicado en el capítulo anterior.

Latidos

La primera corresponde a unos latidos, grabados por Rosa Mª Padilla (http://www.canalincognito.com)/, que se pueden descargar en su página web:

Se oye un sonido continuo de alta frecuencia, y se intuyen unos latidos o pulsos de baja frecuencia. Suponemos que fue tomada en una grabadora analógica, y posteriormente digitalizada a una frecuencia de muestreo de 32 Khz (datos que se obtienen de Goldwave).

Su espectro de frecuencia tiene este aspecto:

Tiene una marcada tendencia de ruido 1/f, y se intuye un ecualizado que le da cierta ondulación al espectro. Probablemente a la compresión (es un fichero MP3) o a un filtrado paso-bajo de 11Khz, la parte de más alta frecuencia se ha perdido. Se ven una serie de picos: Los de más alta frecuencia son una familia de señales, siendo la mayor a 4.42 Khz, otras a ±100, 200, 300... hz, y otras menos intensas a ±50,150,250... hz, y existen sus segundos armónicos en la zona de 9 Khz. Estas frecuencias son las responsables del zumbido de alta frecuencia que se oye en toda la grabación. Si recordamos la interferencia producida por un altavoz conectado a la red eléctrica, sólo vimos el espectro de baja frecuencia. El espectro entero es este:



donde se puede ver una familia similar de picos, aunque a frecuencia superior (15.6Khz el mayor, y el resto a ±100, 200, 300 hz...). Una frecuencia de muestreo de 32 Khz debería ser capaz de muestrear correctamente una frecuencia de 15.6 Khz. El espectro de la interferencia del altavoz estaba muestreado a 44.1 Khz. Si suponemos que es la misma señal, proviniente de un aparato conectado a la red, habría que suponer entonces que no ha sido correctamente muestreada en ninguno de los dos casos, lo que inplicaría que la señal tiene una frecuencia mayor de 22Khz.

El latido es un sonido de baja frecuencia, y su parte de espectro es esta:


Se ve en el espectro que, posiblemente debido a la compresión del fichero, la tendencia de 1/f se trunca, cae bruscamente, y no vuelve a aumentar, que sería lo normal. Aparecen una serie picos, que se pueden intentar clasificar en armónicos: Los armónicos de 486 hz, que por ser los más intensos, podrían ser del motor. Existe otra familia de armónicos a 360 hz, y varios picos dispersos. Por debajo de 200 hz, los picos tiene una relación señal/ruido baja. El único pico por debajo de 200 que sale de forma inequívoca del ruido es el de 50 hz.

En cuanto a los latidos, son sonidos muy graves, de la parte de muy baja frecuencia. Filtrando diversos intervalos de frecuencia, se puede comprobar que el latido se produce principalmente en ese rango por debajo de los 200 hz donde la contribución más clara es de 50 hz. Usando un filtro pasa-banda centrado en esa frecuencia para aislarla, la forma de onda que queda es ésta:



En la gráfica se ve la forma de onda A(t) (en negro) y su amplitud (rojo), y para mayor claridad, debajo está el cuadrado de la intensidad de la onda (azul) (si se me permite, es un "pequeño truco" para poder apreciar visualmente mejor lo que se quiere decir). En ésta última se aprecia muy bien una intensidad baja, que oscila dentro de unos valores que se podría considerar la banda de ruido, o señal de fondo (señalado su borde superior con una línea de puntos), pero en ciertos momentos, la intensidad sube notablemente por encima de esta banda, justo los momentos en que se oyen los latidos. Si los latidos no tuvieran una componente a 50 hz (entre otras frecuencias), entonces no aparecerían estos picos por encima del fondo.

Resumiendo, tenemos:
- Posiblemente, un motor que genera un ruido de 486 hz.
- Posiblemente, interferencia con un aparato eléctrico ¿conectado a la red de 50 hz?, que genera una señal a 4.4 Khz tras el muestreo, con picos satélite a ±50,100,150,... hz
- A muy baja frecuencia (f menor de 200)la frecuencia de 50 hz es la que mejor sobresale por encima del ruido.
- El sonido del "latido" está en la zona de f menor de 200 hz, dominada por ruido, y donde la contribución más clara es la de 50 hz, cuya intensidad sigue el ritmo de los latidos.

¿El latido es producido simplemente por fluctuaciones en las interferencias presentes en toda la grabación?

Matada

El otro ejemplo lo hemos encontrado en la web de www.adimensional.org, grabado por David Garcés. Supuestamente, la psicofonía diría la palabra "Matada". Pueden descargarla desde su sección de grabaciones, dentro del apartado de psicofonías.

Está muestreada a 16 Khz, y en formato MP3.

Merece la pena escucharla varias veces con atención. Las primeras veces, se escucha un ruido continuo (¿el motor?) y tres golpes de sonido que parecen decir "Matada". Con más atención, se escucha un click justo antes de la palabra. Se suele decir que este click es típico que aparezca precediendo a una psicofonía (aunque también hay quien reconoce que no es tan habitual). Si se escucha con más atención, antes del click también se aprecia un susurro, arrastre o ruido.

El sonido tiene un inicio en que sólo se escucha fondo, sin click ni psicofonía, así que lo hemos aprovechado para hacernos una idea de cual es el ruido natural del sistema de grabación. Su espectro:

Se ve la pérdida de información a alta y baja frecuencia, debida probablemente a la compresión. Por debajo de 1.5 khz, se observan sólo unos pocos picos que sobresalen de la banda de ruido, entre ellos: 511, 766 y 1024 hz. Los tres son equidistantes (~250 hz de diferencia entre ellos), aunque sin embargo no aparece la frecuencia de 250 hz, lo que habría hecho que se pudieran considerar como armónicos de 250. En todo caso, estas frecuencias se podrían atribuir al motor.

Por debajo de los 200 hz, se aprecia el ruido 1/f, de donde no se puede afirmar con seguridad que existan señales, ni siquiera la de 50 hz aunque lo parezca, dado que a partir de esa frecuencia el ruido cae a cero, debido (quizás) a la compresión, y se pierde la información.

Respecto a la palabra, su espectro, comparado con el fondo es éste:

Aparecen nuevas frecuencias: entre 152 y 163 hz, entre 200 y 250, siendo la más importante la de 230, y en un rango entre 450 y 600, incluyendo la frecuencia del motor. Parece también que a baja frecuencia se reduce el ruido y se descubre un pico a ~80 hz (160 hz podría ser su segundo armónico, y 240 hz podría ser el tercero, camuflado en el rango 200 a 250 hz), aunque por ser la zona del espectro dominada principalmente por ruido, no es fiable esta apreciación.

Estas frecuencias son las que producen el sonido "Matada". Respecto al click, no se ve en la comparación de espectros, pero se puede aislar en un rango de frecuencias entre 2000 y 3000 hz. Volveremos más tarde sobre él.

Podemos analizar por separado cada frecuencia significativa, haciendo filtrados de pasa banda centrados en cada frecuencia de interés, y ver cómo varía el cuadrado de su intensidad con el tiempo:

Nota: La gráfica de 50 hz se ha multiplicado por 0.1 para reducirla de tamaño, y la gráfica del click se ha multiplicado por 10 para aumentarla, y poder ver todas a la vez. El oído tiene una respuesta distinta a cada frecuencia, de forma que hay frecuencias que pueden ser percibidas con más intensidad o "volumen", aunque su intensidad real sea mucho menor, y viceversa, sonidos con alta intensidad que se perciban muy débiles.

50 hz:
No muestra ningún tipo de patrón, ni tiene correlación alguna con los sonidos que aparecen. Se podría considerar sólo ruido aleatorio.

511 hz:
El (posible) ruido del motor tiene una contribución más o menos constante, con pequeñas variaciones, hasta que llega a la palabra: entonces sufre dos caídas bruscas. Si fuera un sonido o interferencia externa que se añade al fondo, las contribuciones se sumarían a la del motor, pero en cambio, la intensidad baja de forma brusca. Podría ser indicio de que "algo" ha pasado en el motor.

200-250 hz:
Su contribución es sólo ruido, a excepción del momento en que aparece el click, y es la componente principal de la primera sílaba.

150-160 hz:
Es sólo ruido hasta la aparición de la palabra, donde forma las dos últimas sílabas. También parece salir del ruido cuando aparecen los clicks:

Click (2000-3000 hz):
Esta gráfica se halla multiplicada por 10. Al aislar este sonido con un filtro de pasa-banda, aparecen dos nuevos clicks de menor intensidad que estaban escondidos en el ruido. Y curiosamente, justo después aparecen sendas contribuciones (que apenas salen de la banda de ruido) de 150-160 y 200-250 hz, que podrían ser el susurro o arrastre que se oye antes del tercer click (el audible en el sonido original sin filtrar) y la supuesta palabra. Los clicks, están aproximadamente en momentos de tiempo casi equidistantes: t=0.29 s, t=0.61 s y t=1.01 s. Son pocos para poder establecer una periodicidad. Una grabación larga donde se pudieran escuchar varios seguidos podría determinar si es algo aleatorio o periódico. Si fuera algo periódico, probablemente se podría achacar a algún aspecto de la grabadora o la cinta, porque son los únicos elementos que poseen movimientos o funcionamiento de este tipo.

En la anterior psicofonía, se podía ver cómo una posible interferencia electromagnética estaba presente y se podía relacionar con la inclusión. En ésta, aún teniendo otras contribuciones a las que en principio no es evidente asignar un origen, sí se puede ver cómo la frecuencia que viene probablemente del motor está presente, y también se puede relacionar con la inclusión.

Los análisis de psicofonías

En estos dos ejemplos, hemos visto que los ruidos de los que hablábamos en la primera parte pueden efectivamente estar presentes, e incluso ser parte (y puede que importante) de la psicofonía. De ahí la importancia para quien quiera grabar e intentar demostrar la paranormalidad de éstas conozca su equipo. Aquí nos hemos fijado en una sola fuente de ruido, pero puede haber más: la cinta, el micrófono o el lugar, que probablemente sean mucho más importantes, y tengan más peculiaridades.

El gran problema del análisis de psicofonías es que nos encontramos ante un "producto final". Es decir, "algo" ha ocurrido durante la grabación, pero no sabemos el qué. Sólo podemos analizar el resultado final de ese suceso. Y de ahí, estrictamente, lo único que se puede averiguar es lo que finalmente ha quedado: qué sonidos se han registrado, pero no de donde han salido y cómo han llegado allí. De forma indirecta, se puede intuir su procedencia, pero eso depende del conocimiento previo de otros factores, como todas las fuentes de ruido. Al comparar el comportamiento de estos factores con el observado en la grabación es cuando se puede inferir o sugerir que la presunta inclusión puede relacionarse con dicho factor.

Conociendo qué rastro deja el motor y una interferencia electromagnética, hemos detectado ambos en dos psicofonías, lo que permite colocar algunas piezas del puzzle.

Quienes sostienen hipótesis acerca del Más Allá, telepatías, partículas cuánticas o impregnaciones ambientales, deberían determinar qué rastros podrían dejar éstas en una grabación, para poder compararlo su "producto final". Si de verdad alguno desea demostrar alguna de éstas hipótesis y revolucionar la ciencia, es por donde debería empezar. Pero grabar por grabar indiscriminadamente, es la mejor forma para maravillarse por no encontrar una explicación lógica.