En
una ocasión hablamos de un artículo de
El País Semanal, donde hacían un reportaje acerca de
Rupert Sheldrake, y sus teorías (por llamarlas de alguna manera), acerca de la telepatía, inconsciente colectivo y demás zarandajas.
Una de sus sorprendentes afirmaciones es que una persona es capaz de saber quién está llamando por teléfono antes de responder. El caso es que hay gente que incluso cree que estas afirmaciones son ciertas más allá de lo esperado por azar, y así, hemos encontrado a dos profesores de psicología de la
Universidad de Amsterdam que han intentado replicar experimentos previos de Sheldrake, cuyo resultado se puede leer en un artículo titulado
"Who's calling at this hour? Local Sidereal Time and telephone telepathy" (.pdf) (
"¿Quién llama a esta hora? Telepatía telefónica y Hora Sidérea Local "), perpetrado por Eva Lobach y
Dick Bierman, y publicado en los proceedings una Convención de la Asociación Parapsicológica en 2004.
La afirmación original de Sheldrake es que el hecho de que una persona adivine quien está llamando antes de coger el teléfono no es por azar, sino por telepatía. ¿A quien no le ha pasado que está pensando en alguien, y justo en ese momento esa persona llama por teléfono?. De lo que no se suele acordar la gente es de aquellas veces que la persona que llama no es en quien pensábamos.
Pero ahí no acaba todo. Se supone además que se encontró experimentalmente una correlación entre la hora sidérea local y la capacidad de saber quien llama, habiendo una hora "punta" a eso de las 13.30 (hora sidérea local ).
Así que ni cortos ni perezosos, Lobach & Bierman escogieron 6 personas que decían tener ese tipo de experiencias. Cada una de ellas, escogió 4 amigos o familiares, que les llamarían por teléfono según el azar dictado por un dado lanzado por un experimentador. Antes de coger el teléfono, la persona decía en voz alta quien estaba llamando, cogía el teléfono, y otro experimentador anotaba si era un fallo o un acierto.
Se hicieron 36 intentos para cada persona, repartidos de esta forma : 3 series de 6 intentos en hora punta (un total de 18 intentos), y 3 series de 6 intentos en hora valle (otros 18 intentos), y los resultados fueron los de esta tabla:
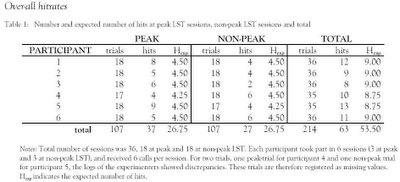
que a falta de mayor detalle en cada una las 3 sesiones de 6 intentos, lo tomaremos como que hubo una sesión de 18 intentos en la hora punta, y una sesión de 18 intentos en hora valle a cada persona.
Lo primero que resulta curioso comprobar es que 4+4+2+6+4+6 (
hits en
non-peak hour) no son 27 sino 26. En fin, un errorcillo de imprenta, suponemos.
Hay dos valores no registrados, debido a que el registro del experimentador que determinaba quien llamaba, y el del que comprobaba el acierto eran distintos en la hora de llamada anotada, pero en el texto nos indican que había sido un acierto (y que así constaba en los registros). Y como somos buenos, vamos a aceptar el acierto.
Hay varias formas de tratar los datos. Una de ellas es considerar que cada persona representa una serie de 18 o 36 intentos de la que ha obtenido un valor, y luego se ha calculado la media de estas 6 series para determinar si existe un efecto real. Este es el enfoque que han escogido los autores, y que vamos a seguir.
Los resultados según esta forma de tratar los datos, es que en total se obtuvo un 29% de aciertos (una media de 10.8 sobre 36 intentos), más que el 25% esperado por azar (una media de 9 sobre 36).
Respecto a la influencia de la hora, se obtiene que en la hora punta la media de aciertos era de 6.33 sobre 18 (35%), y en hora valle 4.5 sobre 18 (25%, que coincide con la media esperada por azar).
Ahora viene la pregunta del millón ¿estos datos se pueden atribuir a una "tirada con suerte" de azar puro y duro, o hay un efecto real de telepatía telefónica?. Para evaluarlo, existen tests que determinan cual es la probabilidad de que el resultado obtenido no haya sido debido a la teoría que se está testando. El más común es el de
chi-cuadrado (χ2), pero que con pocas muestras puede ser impreciso. En el artículo usan el
test t de Student, más útil para pocas muestras. En ambos casos, de la prueba se obtiene un valor, que se compara con uno que está tabulado en función del número de datos de la estadística experimental (grados de libertad), y del nivel de confianza. Éste nivel de confianza se suele tomar del 95% (p=0.05 o p=0.95 según el lugar que se lea). Si el valor de la prueba es menor que el tabulado, entonces podemos pensar que nuestra teoría no es falsa con un margen de confianza del 95%. En caso contrario, habría que tomar en serio la posibilidad de que la teoría es falsa.
En nuestro caso, la teoría a testar es que los resultados son producidos por azar, y lo que habría que obtener en estos tests es un resultado mayor que los tabulados para pensar que puede existir otra teoría.
El test de chi-cuadrado
se puede comprobar que da negativo en los tres casos (hora punta, hora valle y total). El
test t de Student en el artículo da un resultado positivo tanto en hora punta como en el total. No hemos podido encontrar una forma de comprobarlo, así que vamos a optar por un análisis más de andar por casa, con menos rigor, pero más ilustrativo.
Podemos agrupar los datos de dos formas: series de 18 intentos, y series de 36 intentos. En cada serie, hay una probablidad de acertar un número determinado de veces. Aunque la cuenta de la vieja nos dice que hay que acertar 4.5 veces para series de 18 intentos (9 para 36), en realidad, nada nos impide acertar 10 veces, y que siga siendo por puro azar. Pero si realizamos un número elevado de series, y anotamos cuantas veces acertamos 1, 2 , 3... o 18 veces, se pueden obtener distribuciones de aciertos tal que así:
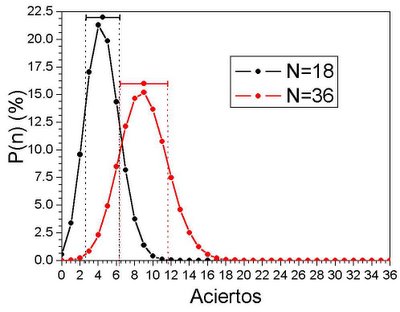
Distribución que corresponde estrictamente a lo esperado por azar. De aquí se pueden hallar dos parámetros muy importantes: la media y la desviación.
La media corresponde a lo que calculamos por cuenta de la vieja (4.5 para 18 intentos, 9 para 36), pero también importante es la desviación, que nos indica entre qué valores varía el número de aciertos cada vez que hacemos una prueba, o entre que valores se reparten con mayor frecuencia los aciertos.
Para series de 18 intentos, la media teórica es de 4.5, y la desviación de 1.83 (marcado en la gráfica como el punto con las barras, 4.5 ± 1.83), lo que quiere decir que el 66% de las veces, se acertarán entre 4.5-1.83=2.87 (3 veces) y 4.5+1.83=6.33 (6 veces), y el 95% acertará entre 1 y 8. Para series de 36 intentos, la media teórica es 9 ± 2.6
Sin embargo, en este artículo se han hecho sólo 6 series, lo que parecen pocas, y es fácil obtener resultados de medias que no correspondan a la teórica. Para obtener los valores teóricos, habría que repetir las series un elevado número de veces.
En el caso de las 6 series de 36 intentos, la media determinada es de 10.8 ± 2.13. ¿Es posible obtener este valor sólo por azar?. Para ello, hemos generado por azar valores de 6 series de 36 intentos, y los hemos comparado con la media teórica y la obtenida por Lobach & Bierman:
El punto representa el valor medio, y las líneas representan la desviación a cada lado. Y sí, el valor obtenido experimentalmente se puede obtener sólo por azar. Además, el valor experimental entra dentro del rango de media±desviación teórico, lo que suele ser significativo de que los valores son coherentes con la misma teoría (en este caso, que los valores se obtienen por puro azar).
Igual podemos hacer para las 6 series de 18 intentos, donde se obtenía en la hora punta un valor de 6.33±1.75, y para la hora valle 4.5±1.51:

De la hora valle no hace falta hablar.
En el caso de la hora punta, el valor está justo en el límite de entrar en el rango de 4.5±1.83 teórico, aunque sin embargo, sigue siendo posible encontrar resultados parecidos sólo por azar.
El mayor problema del trabajo de Lobach & Bierman, está en que a pesar de hacer un total de 216 intentos, se han agrupado en sólo 6 series, una por persona, de donde se obtienen los datos. Haciendo tan pocas series se pueden obtener una gran variedad de medias (con sus desviaciones), así que ¿cuál es la probabilidad de haber sacado estas medias sólo por azar o por el contrario, que haya salido porque existe un fenómeno real, desconocido y negado por la malvada ciencia oficial?. Eso es lo que miden los test chi-cuadrado y t de Student de que hemos hablado antes.
Aquí vamos a hacerlo "a lo bruto". Vamos a hacer un número elevado de veces un experimento de 6 series de 18 y 36 intentos, y cada vez, vamos a calcular la media. Luego contamos las veces que ha salido cada media, agrupadas en intervalos de 0.5, es decir, contamos el número de veces que la media sale entre 4 y 4.5, entre 4.5 y 5, etc... Para series de 36 intentos, el resultado es:
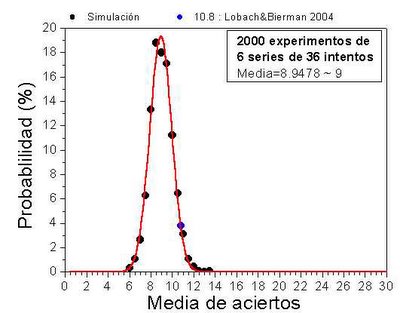
Todos los valores obtenidos se distribuyen alrededor de la media verdadera (9), entre 6 y 14. Si en vez de 6 series, hubieran sido 12, 24 o 527 series de 36 intentos, esta distribución hubiera sido más estrecha, es decir, habría menos dispersión en los valores que se pueden obtener como media. En todo caso, el punto experimental resulta tener una probabilidad de un 3% para salir en un experimento sólo por azar, mientras que la media verdadera (9 aciertos), tiene menos del 20% (1 de cada 5) de probabilidad de salir.
Es interesante ver como a pesar de ser lo esperado por azar, es más fácil que salga cualquier otro valor (80%) distinto a la media (20%). Cualquier medida de cualquier experimento se distribuye siempre alrededor de un valor verdadero como el mostrado arriba. Por eso es necesario repetir siempre los experimentos, comprobar si el valor obtenido experimentalmente entra o no dentro de la distribución de valores y determinar la media real. También es importante el diseño del experimento para que la anchura alrededor de la que se distribuyen los valores sea lo más estrecha posible, esto es, tener un experimento con la resolución necesaria. Si de pronto un valor no entrara dentro de la distribución, entonces se podría sospechar que ha habido algún fallo en el experimento, o que la teoría utilizada es incorrecta (en ese orden).
Pero en nuestro caso, el valor de Lobach & Bierman entra dentro de la distribución esperada por azar. Sólo si tras un número elevado de experimentos, los valores se agruparan en torno a este 10.8 en vez del 9 teórico, se podría decir que hay un efecto real. Cómo solo tenemos un dato, no se puede concluir que el efecto exista, porque no hay datos suficientes.
Podemos hacer lo mismo para el caso de 6 series de 18 intentos, donde un valor estaba en el límite de lo esperado por azar:

y se puede ver que mientras un valor (el de la hora valle) está en la media, el otro (hora punta) a pesar de estar cercano al límite, todavía entra dentro de lo esperado por azar. Una vez más, sólo es un punto, y no es posible concluir la existencia del fenómeno, a menos que se repita el experimento un número elevado de veces, y las medias de cada uno se agrupen en torno a 6 aciertos.
Repeticiones por cierto, que implican hacer colaborar a las mismas personas cada vez, y puede que no todas tengan ganas de colaborar tanto. Nadie dijo que investigar fuera fácil, ni cuestión de una tarde.
Las conclusiones
En realidad, el estudio es más chapucero de lo contado aquí. Resulta que a la hora de hacer las llamadas, hubo ocasiones en que no todas las personas que iban a llamar estaban disponibles. Es decir, había veces que mientras que la persona llamada intentaba adivinar entre 4 personas distintas, en realidad sólo recibía llamadas de 2 personas porque las otras estaban en la ducha, o dumiendo. Y hubo dos resultados que se anularon por problemas en los registros (aunque aquí los hemos considerado válidos). Esto hace que los valores no sean comparables entre sí y haya que hacer
"ingeniería combinacional" para relacionarlos.
Por otro lado, el diseño del experimento tampoco es del todo acertado. Ante todo, se presupone que las personas tienen la misma capacidad de adivinar quien les está llamando. Imaginemos que una de ellas sí tiene esta capacidad, pero las otras 5 no. Al considerar todos los resultados juntos, en realidad se está "ocultando" la capacidad de esa persona entre el "ruido" aleatorio de las otras 5. Lo correcto hubiera sido hacer muchas series, de muchos intentos a cada persona por separado, y no una sola serie de 18 o 36 intentos, según se interpreten los datos, para determinar si esa persona tiene o no la capacidad.
Pero todo esto no es obstáculo para que los autores concluyan que:
"Los resultados muestran una débil evidencia para apoyar la hipótesis de que la Hora Local Sideral afecta a un fenómeno de cognición anómala como la telepatía telefónica. Nuestra muestra era pequeña, y el alto número de sesiones con irregularidades debilitaron aún más la potencia de nuestros análisis. Sin embargo, los resultados son prometedores y se garantiza que habrá réplicas de ellos.
(...)
Los resultados apoyan la existencia de la telepatía telefónica. En general, nuestros participantes acertaron correctamente más de lo esperado por azar. La evidencia no es tan impresionante como el 45% de Sheldrake(2003), sin embargo puede ser debido a su preselección de participantes a través de un estudio previo, mientras que nosotros empleamos un criterio de selección flexible incluyendo sólo a aquellos participantes que declararon haber tenido experiencias de telepatía telefónica en el pasado"
que traducido al castellano, viene a decir:
"Los resultados son pobres porque la muestra era pequeña, la mayoría de series presentaban irregularidades, y ni siquiera sé a ciencia cierta si los participantes tenían la capacidad que decían, por lo que un análisis puede dar cualquier cosa; pero como ha dado un resultado que me gusta a mí, la hipótesis queda apoyada."