Malas vibraciones

El origen de las vibraciones

Anteriormente establecimos una hipótesis acerca de cómo una vibración del cabezal de escritura podría afectar en una grabación. Como toda hipótesis que pretenda ser válida, debe basarse en una realidad que sea posible comprobar, y determinar si es lo suficientemente realista (aunque tenga aproximaciones o simplificaciones), o si hace falta modificarla en algún punto.

Supusimos que las oscilaciones del cabezal eran tales que se acercaba y alejaba de la cinta magnética, de forma que modulaba la amplitud del ruido, lo cual describían estas ecuaciones:

Donde r0 es la distancia en condiciones normales y r la distancia cuando vibra el cabezal. ¿Se acerca esto a la realidad?

Veamos los cabezales de un radiocassette:

Al pulsar la tecla de grabar, bajan los dos cabezales, y una rueda de goma. La rueda gira para tensar y arrastrar la cinta. Los cabezales por su parte llegan a hacer contacto con la cinta, y la empujan. En el caso del cabezal de escritura, la cinta queda además atrapada entre él, y un fleje (o muelle) que tiene la propia cinta. Este fleje ejerce una fuerza hacia el cabezal, de forma que aprisiona la cinta, y los pone en buen contacto.

Cuando hay vibraciones que desplacen ligeramente el cabezal de arriba a abajo, el fleje absorbe esa vibración y mantiene el contacto entre ambos.

Al tacto, el fleje no es un muelle "duro", sino que se desplaza con facilidad. Con una vibración fuerte, o un golpe seco, el fleje podría "rebotar" demasiado, rompiendo el buen contacto, y separando la cinta del cabezal. Más aún, la rueda tensora baja y sube a la vez que el cabezal, por lo que un golpe o vibración fuerte podría hacer que se desplazara ligeramente y dejar de tensar brevemente la cinta. Esto también dificultaría el buen contacto entre cinta y cabezal.

Notar que el cabezal de borrado no tiene un fleje o muelle que absorba o minimice las vibraciones, por lo que el borrado podría no ser correcto en una de estas vibraciones, y dejar rastro de grabaciones anteriores. Es una posibilidad que no vamos a tener en cuenta en lo que sigue.

Para una descripción más real de las vibraciones hay que tener en cuenta que la cinta ya está en contacto con el cabezal, y por tanto, no va a estar más cerca del valor nominal r₀.

Aclaración: "en contacto", no quiere decir que r₀=0. La cinta es una lámina de plástico, con varios recubrimientos, y entre el material magnético y el cabezal hay una capa protectora, para evitar que se raye o deteriore. Igualmente, como "distancia cero" se toma el centro del entrehierro del cabezal donde se surge el campo magnético, y la cinta va a pasar por debajo del entrehierro:

Esto quiere decir (para quien lo quiera calcular), que si la oscilación hace que r sea menor que r₀, entonces se debe tomar el valor r0. En la siguiente gráfica, la línea negra representa el valor de r(t), mientras que la roja es la variación del campo magnético que produciría: al alejarse el cabezal, disminuiría el campo, y por tanto el valor de la magnetización que quedaría en la cinta:

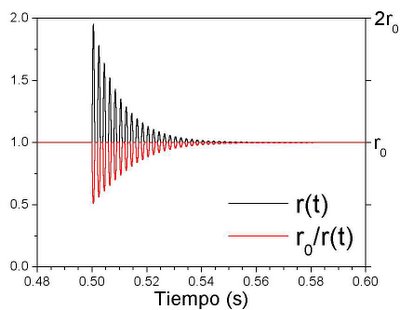
¿Qué valores se pueden poner para simular sonidos? Para empezar, el valor de r₀ es indiferente. El hecho de definir la amplitud A como se hizo, permite que la cantidad [r₀/r(t)] sea independiente de r₀.

Los otros valores son libres para experimentar aquel que quiera. La frecuencia determina el tono del click. La constante de tiempo t₀ está relacionado con el tiempo que tarda en desaparecer el sonido. Cuanto menor sea, menos tiempo tardarán en desaparecer las oscilaciones, y más apariencia de golpe tiene el sonido

Si alguien quiere probar a simular, las instrucciones son estas:

- Generar un ruido marrón con una intensidad arbitraria: Escoger un valor arbitrario de la magnetización M₀, de la amplitud A (A=1 es suficiente), de la frecuencia f, de t₀ y un valor inicial de la fase (fi) de la intensidad. Calcular un número aleatorio entre 0 y 1. Si es mayor de 0.5, sumar a la fase un valor determinado. Si es menor, restarlo.
- Calcular la oscilación del cabezal y la cantidad [r₀/r(t)]. Si es mayor de 1, entonces igualarlo a 1.
- Calcular el valor final como M₀·cos(fi)·[r₀/r(t)]

¿Es este modelo realista?

Hay que reconocer que las cintas vienen bien preparadas para soportar vibraciones, pero sólo hasta un límite. Si hay golpes, o vibraciones fuertes, ya sea por llevar la grabadora en la mano, o colgada del cuello[1], si está por un suelo que transmite bien vibraciones mientras la gente pasea a su alrededor sin prestar atención[2], o se cae un objeto al suelo, no es imposible que pudiera suceder.

Hay que tener en cuenta que las oscilaciones tienen una amplitud del orden de r₀. Y esta distancia, aunque no es cero, es muy pequeña (menos de 0.1 milímetros, por poner un valor). Cuanto más pequeña, más facilidad hay de que en algún momento la cinta se pueda separar hasta por ejemplo r=2r₀ (que serían 0.2 milímetros)

Hemos supuesto una vibración simple, de una sola frecuencia. En un modelo más real, esta vibración podría ser cualquier función que cumpliera dos requisitos:
- Que se amortigüe con el tiempo (recupera el valor previo a la perturbación)
- Que sea periódica. Siendo así, se puede expresar como una suma de senos y/o cosenos de distintas frecuencias.

Se podría escribir algo así

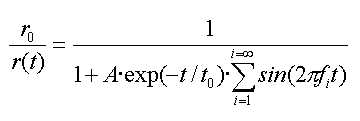
Es decir, la oscilación como un conjunto de frecuencias, que no tendrían por qué ser armónicas entre ellas, ni estar relacionadas, y que dependería del aparato de grabación (cómo transmite las vibraciones su carcasa y mecanismo que sujeta los cabezales) y del fleje de la cinta. Para la misma cinta y aparato, el click debería ser siempre igual.

Por hacer una prueba, he aquí un click generado con 3 frecuencias distintas arbitrarias. Suena más real que un click de una sola frecuencia (500hz).

Y para comparar, el click de verdad

Vibraciones en el micrófono

Hay que reconocer que la vibración del cabezal es un tanto complicada. Las cintas, y el sistema entero está diseñado para absorberlas, así que sólo parecen posibles vibraciones fuertes, debidas a un golpe o movimientos bruscos.

Ya hemos mencionado alguna vez que emplear un poco de método y rigor hace posible estudiar cualquier hipótesis y encontrar resultados con los que saber las posibilidades reales de que una hipótesis así no sea errónea. En este caso, si bien las vibraciones no son imposibles, si parecen un poco difíciles de ocurrir.

Vamos buscar otra hipótesis más probable, modificándo ésta ligeramente. Mantenemos la idea básica de una oscilación amortiguada, pero en vez de suponer que ocurren en el cabezal, vamos a suponer que es en el micrófono.

Los micrófonos más extendidos (y usados por expertos en psicofonías), son del tipo dinámico. Están basados en una membrana, a la que está pegada una barra ferromagnética rodeada de una bobina de cable. A una corta distancia se coloca un imán potente. Cuando llega un sonido, la membrana desplaza la barra metálica. Al estar dentro del campo magnético del imán, la vibración produce una señal eléctrica en la bobina, que es la que se recoge en un amplificador para ser grabada. El funcionamiento es exactamente el inverso a un auricular o altavoz. Incluso un pequeño auricular puede servir de micrófono. Es una aplicación directa de la Ley de Faraday (nada que ver con las jaulas), una de las cuatro ecuaciones de Maxwell que explican el electromagnetismo, y por las que se rigen las grabadoras y micrófonos.

Pincha aquí para ver un ejemplo de cómo funciona un altavoz. El micrófono funcionaría de forma inversa.

Al contrario que en el cassette, que procuraba mantener la cinta magnética en contacto con el cabezal, en un micrófono (o altavoz) lo que interesa es que se pueda mover y vibrar fácilmente con el sonido, para convertir ese movimiento en electricidad. Esto hace que sea más sensible a vibraciones y golpes que el cabezal.

Puesto en ecuaciones, recordamos que la magnetización en una cinta dependía de dos factores: la distancia al cabezal (que ahora suponemos constante) y la intensidad eléctrica, que ahora no va a modular el ruido, sino que es una señal que se va a añadir a éste:

donde A es otra vez la amplitud de las vibraciones, definida de esta forma:
Si A=1, la oscilación produce una intensidad que varía entre I=-I₀ hasta I=I₀
Si A=2, la oscilación de la intensidad va desde I=-2I₀ hasta I=2·I₀ . (Que I sea negativo no representa ningún problema)

De esta forma, el cálculo es independiente del valor de I₀

Al igual que antes, el modelo se puede hacer más real suponiendo que la oscilación no ocurre a una sola frecuencia, sino que puede ser una función arbitraria, con mezcla de varias frecuencias.

Click de una sola frecuencia (f=500 hz, t0=0.05).
Click con tres frecuencias.

Juntando sonidos

Hay una gran diferencia entre las dos formas de generar el sonido. Si suponemos que el sonido se genera por una vibración del cabezal, el sonido aparece como una modulación del ruido de fondo, el cual incluiría el ruido del motor. En realidad, es una atenuación del ruido de fondo, excepto de las frecuencias que generan la vibración.

Si suponemos una vibración del micrófono, entonces tenemos un ruido que se suma sin alterar el resto de sonidos ya presentes, se añaden nuevas frecuencias.

He aquí dos ejemplos en los que se ha añadido una frecuencia simulando un ruido de motor a 200 hz:

Click del cabezal
Click del micrófono


Bricomanía: un micrófono casero

He aquí la forma de hacerse un "micrófono" casero: Busca un hierro o material ferromagnético, como un destornillador. Enrolla un cable, y conecta los extremos a una clavija conectada a la tarjeta de sonido:

Ahora busca un imán potente, como el de un altavoz viejo, y acércalos. Colócalos de tal manera que la bobina pueda vibrar. Por ejemplo, aquí la he puesto sobre un soporte metálico hueco:

que golpeado suena tal que así: click

Dependiendo donde se coloque (y cómo), el sonido será de una forma u otra. Por ejemplo, sobre un vaso:

que al golpearlo suena de esta otra forma: click

Las frecuencias o sonidos que puede registrar un dispositivo (o apaño) como éstos depende de las propiedades elásticas de cada material; es decir, dependen de cómo vibran, y cada objeto y material tiene sus vibraciones características, también llamadas resonancias. La barra o el vaso son muy rígidos, y vibran poco, comparados con un micrófono real, donde la membrana está diseñada para tal fin, y permite registrar un amplio rango de frecuencias, que viene siempre documentado en un gráfico que muestra la intensidad relativa con que registra de cada frecuencia

Espectro de un micrófono dinámico Sennheiser 825-s

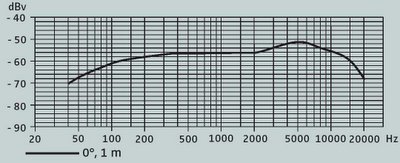
Si hay un golpe en la carcasa del micrófono, éste se transmite a la membrana, de igual forma que se transmiten las vibraciones desde un vaso a la punta del destornillador, y puede quedar registrado.

Resumiendo

En cualquier sistema siempre hay elementos que son susceptibles de vibrar, y que en algunos casos pueden influir en una señal eléctrica o magnética, y en cómo se registran estas señales. Prueba de ello son las medidas de seguridad que se toman en una cinta, por ejemplo, para minimizar estas vibraciones.

Nota: El click "de verdad" está cogido de la sección de psicofonías de Adimensional (click_metalico.mp3). En el sonido completo se aprecia como después del click, aumenta el nivel de ruido, como si se hubiera cogido la grabadora para subir el volumen en mitad de la grabación.

[1] http://www.aaevp.com/articles/articles_about_evp1.htm

"At one point I discovered, to my joy, that if I hung my recorder around my neck and walked around my flat as I was recording, the EVP utterances became magnified and much more abundant."

Tina Laurent, Asociación Americana del Fenómeno de Voces Electrónicas

[2] http://jabber-hispano.org/mesias/chat/seip/fomalhaut1.htm

"Por protocolo y por lo que pudiese registrarse, dejamos un grabador en marcha, a la cual no prestamos mucha anteción durante nuestra breve estancia (...)
No sólo los registros psicofónicos fueron desmesurados, sino que también fueron contundentes, objetivos y dennotaban cierta proximidad hacia nosotros, algo que nos sobrecogió y que de la misma forma hizo cuestionarnos numerosas preguntas;
¿Por qué esa noche, cuando apenas teníamos controlado el medio?"

David Ruiz, investigador de psicofonías

Click!

Hay que ver lo que dan de sí las psicofonías.

En anteriores entradas estuvimos viendo qué tipo de ruido eléctrico y electromagnético puede haber en una grabadora, y cómo estos ruidos podían estar a su vez presentes en los sonidos que identificaban a las supuestas psicofonías. También vimos cómo una jaula de Faraday no es un elemento mágico, sino que tiene sus limitaciones y puede dejar pasar radiación externa, por muy perfecta que se construya. Ahora vamos a tratar otro tipo de ruido, en concreto qué tipo de ruido o "huella" puede dejar una vibración del cabezal de grabación.

Para ello vamos primeramente a conocer cuál es la física en la que se basa el proceso de grabación de una cinta, que siempre es interesante saberlo.

Magnetismo

Todos sabemos que la materia está compuesta de átomos. Éstos átomos, en su forma más simple, se pueden entender como un núcleo central con carga positiva alrededor del cual giran electrones con carga negativa. Este giro es por definición una corriente eléctrica, que a su vez genera un campo magnético. Así, cuando se habla de magnetismo, la forma más simple de imaginar la materia es como compuesta por una multitud de pequeños imanes llamados dipolos magnéticos, que se caracterizan por tener un valor (momento dipolar, u) y una orientación, o sentido en que el campo magnético atraviesa el átomo:

En un material sólido, todos estos dipolos tomados en conjunto se describen por una propiedad llamada "magnetización", que llamaremos M, que describe el valor y orientación promedio de todos los dipolos. Si el material tiene una densidad N (átomos/m³), entonces, M=N[u], donde [u] es el promedio de todos los dipolos considerados. En ausencia de un campo magnético (que llamaremos H), todos estos dipolos están orientados al azar, de forma que en promedio, los campos creados por cada uno se cancelan mutuamente, y entonces [u]=0 y M=0.

Cuando se aplica un H externo, el valor u cambia su valor u orientación de forma que que tomado en promedio este cambio propicia la aparición de una magnetización neta. La respuesta depende del tipo de material.

Tenemos primeramente materiales diamagnéticos: al aplicar un H, éste afecta a la velocidad de giro de los electrones, de forma que todos los dipolos cambian su valor,(pero no su orientación) para oponerse al campo H que le está afectando: Se consigue una magnetización neta negativa, que crea un campo magnético en sentido contrario a H. Si el dipolo está originalmente alineado en la dirección del campo, entonces su momento dipolar se reduce, y si está en sentido contrario, entonces aumenta.

En segundo lugar, tenemos materiales paramagnéticos: además del cambio en el giro de los electrones, los dipolos se reorientan para colocarse alineados con el campo H, de forma que ahora al tomar el promedio de los momentos dipolares no se cancelan, sino que se refuerzan, apareciendo una magnetización positiva (crean un campo en el mismo sentido que H).

En estos dos tipos materiales, M desaparece cuando se elimina H. Pero tenemos un tercer tipo de materiales, que son los que nos interesan de verdad, los ferromagnéticos: Se comportan como los paramagnéticos, pero son capaces de mantener la magnetización cuando se elimina el campo magnético que la crea. Si no existieran estos materiales, no existirían los imanes permanentes, ni motores de grabadoras, ni las cintas de cassette donde grabar psicofonías.

En estos materiales, unos pocos dipolos crean un campo tan fuerte que son capaces de hacer orientarse a los que tienen en su entorno más cercano. De esta forma, el material se divide en muchas zonas, más o menos grandes llamadas dominios, con una magnetización neta, pero con distinta orientación, de forma que tomado en su conjunto, el material puede tener una magnetización nula. Al aplicar un campo externo, algunos de estos dominios se reorientan para alinearse con H, creando una M positiva. Cuando se quita el campo, permanecen con esa orientación, y el material mantiene una magnetización total distinta de cero.

Esta figura representa la curva típica de un material ferromagnético. Representa el valor de M en función de H

Si partimos del punto a de la gráfica, es decir, cuando M=0, y aplicamos un campo magnético externo pequeño, algunos dominios se reorientan creando una magnetización, que se mantiene al retirar H. El valor de M aumenta con H, hasta que llega al punto b, donde todos los dominios estarían totalmente orientados, y alcanzaríamos un valor de saturación, que no se puede superar porque no quedan dominios o dipolos que orientar. Al eliminar H, siempre hay un pequeño descenso del valor de saturación de M debido a que por temperatura, algunos dipolos pueden desorientarse, quedando un valor de la magnetización de saturación cuando H=0, que se llama magnetización remanente, Mr (punto c)

Si ahora aplicamos un campo H en sentido contrario, la magnetización se reduce poco durante un pequeño intervalo, hasta que el campo es lo suficientemente intenso como para comenzar a reorientar los dominios. En esta reorientación, hay un punto (punto d) para el cual se puede anular M, es decir, tenemos tantos dipolos orientados en un sentido, como en el contrario, y por tanto el promedio es cero. El valor de este campo Hc, es llamado campo cohercitivo. Si se aumenta más la intensidad del campo, los dominios se siguen reorientando hasta alcanzar de nuevo la saturación, pero esta vez en sentido opuesto (punto e). Este tipo de curva es típica de materiales ferromagnéticos, y se llaman curvas de histéresis, que son importantes dependiendo del uso que se le de al material.

Cintas de cassette

Una cinta de cassette es un material ferromagnético, que se magnetiza para "recordar" la información. Un sonido se convierte en electricidad. Esta corriente eléctrica se convierte en un campo magnético, y éste en un valor de magnetización sobre la cinta. A la hora de reproducir, la magnetización crea un campo magnético, que genera una corriente eléctrica que es transformada en sonido.

Un cabezal de grabación es como en la figura: una espira, enrrollada en un hierro que tiene un hueco en el otro extremo.

La corriente por la espira crea un campo magnético que es guiado por el hierro. Al llegar al hueco, el campo magnético sale de éste, creando un campo no solo en el hueco, sino también alrededor. Este campo de alrededor es el que magnetiza la cinta. La magnetización producida depende de la intensidad del campo magnético, que a su vez depende de la intensidad de la corriente eléctrica de la espira.

La cinta se divide en pequeñas zonas con dominios que mantienen la magnetización. Al grabar, a cinta pasa primero por un cabezal de borrado, que provoca una magnetización de saturación en cada uno, pero con una orientación aleatoria, de forma que sólo se obtiene ruido sin información. Al tener cada zona una magnetización previa, no se puede grabar directamente la señal, ya que el resultado final depende del estado inicial.

Dependiendo del valor obtenido en el borrado, al aplicar un campo con el valor marcado por la línea de puntos, se podría obtener una magnetización final en el grabado entre C y D. Como esto no es aceptable, en el grabado se añade una señal alterna de alta frecuencia (referida como bias) que recorre el ciclo entero de la histéresis, y hace que en promedio la magnetización sea nula. De esta forma, cuando no hay señal a grabar, la magnetización final es cero. Si hay señal, entonces el valor promedio se desplaza hasta una magnetización proporcional a ésta.

Más información sobre el grabado de cintas, aquí.

Vibración del cabezal

La magnetización de la cinta depende de la intensidad de campo magnético que llega a la superficie de la cinta, y que es proporcional a la señal que se quiere grabar. Las condiciones de trabajo son además tales que hay linearidad entre M y H: es decir, si se aumenta al doble H, entonces M también aumenta el doble (siempre que no superemos el valor de saturación). Además, el campo magnético creado por una espira es proporcional a la intensidad que va por ella, así que al final, la magnetización será directamente proporcional a la corriente I que va por la espira del cabezal.

La intensidad de campo magnético depende no solo de la intensidad de la corriente, sino también de la distancia entre el cabezal de grabado y la cinta (r). A mayor corriente, mayor campo, pero a mayor distancia, menor intensidad. Se puede escribir la dependencia de M con I y r:

(donde k es una constante. Supondremos 1/r porque es el caso "más favorable": la disminución de M es más lenta que si fuera 1/r², 1/r³, o cualquier otra potencia mayor que 1)

Para grabar una señal dependiente del tiempo, M debe variar entre dominio y dominio de la cinta, lo cual se hace normalmente a través de I. Si solo se está grabando ruido, la intensidad se puede escribir de esta forma:

donde I₀ es la amplitud del ruido, y fi(t) es una fase aleatoria. Si el cabezal se mantiene a una distancia r₀ constante de la cinta, la magnetización que queda grabada es simplemente un ruido de amplitud constante kI₀/r₀:

¿Qué ocurre al desplazar el cabezal, por una vibración o un golpe?

Si suponemos un desplazamiento muy pequeño, y que además éste tiende a recuperar su posición inicial a una distancia r₀ de la cinta, r(t) se puede describir de la forma más sencilla así:

Representa una oscilación de frecuencia f₀ en torno al valor r₀ que se va apagando con una constante de tiempo característico t₀, hasta recuperar el valor constante normal. A es la amplitud del la oscilación, entendida de esta forma:

Si A=1, entonces la oscilación tiene una amplitud r₀, y r(t) varía entre 0 y 2r₀.
Si A=2, entonces la oscilación tiene una amplitud 2r₀, y r(t) varía entre -r₀ y 3r₀

Y así sucesivamente... Un valor menor que cero no tiene sentido. Cuando r=0, hay que suponer que el cabezal empuja la cinta, y se la lleva con él manteniendo la distancia constante, hasta que vuelve a rebotar hacia arriba.

¿Qué valor puede tener r₀, la distancia entre cabezal y cinta? Muy pequeña. Por hacernos una idea, pongamos que medio milímetro (que posiblemente sea demasiado). Con A=1, la distancia del cabezal oscilaría entre 0 y 1 milímetros. Si r₀=0.1 mm, entonces oscilaría entre 0 y 0.2 mm

Ahora la magnetización se puede escribir de esta forma:

Si a partir de la primera ecuación, multiplicamos y dividimos por r₀, y reagrupamos los términos, nos queda la magnetización original sin vibración, que tiene una amplitud M₀, pero modulada por la cantidad r₀/r(t). Esto es interesante: la vibración es un ruido que no se añade (se suma) al ya existente, sino que lo modula, hace variar la amplitud del ruido original.

Imaginemos que se está grabando una señal de ruido constante, y al coger la grabadora, o por una vibración que se transmite por el suelo, el cabezal sufre una vibración, que se amortigua y desaparece en menos de medio segundo. La magnetización sufrirá esta modulación, aunque la corriente sea constante. Pero al reproducir la cinta, si el cabezal mantiene una posición fija, la modulación del ruido producirá un cambio en la intensidad eléctrica, se interpretará como tal, y será convertida a sonido en los altavoces: la vibración se interpretará al reproducir como si se hubiera grabado un sonido.

¡Click! Probando un dos tres... ¿Se me oye?

Por no ser muy pesados, en una segunda parte veremos que al simular estas vibraciones aparece este sonido:

Click

Que recuerda bastante a los clicks que se escuchan en algunas psicofonías, y que los entendidos del tema dicen que es habitual que aparezcan justo antes de oírse una psicofonía de las de verdad.

No cambien de canal.

El mito de la jaula de Faraday

Existen palabras mágicas que de pronto parecen explicar todo, como "Mecánica Cuántica" (con mayúscula, que si no, pierden sus poderes). Y como no podía ser de otra manera, también existen artilugios mágicos que de pronto hacen que toda explicación racional pueda ser deshechada, de una forma que incluso se podría llamar dogmática. Es el caso de las Jaulas de Faraday (con mayúscula, claro) cuando el tema de discusión son las psicofonías. Sólo el hecho de incluir una de éstas hace imposible la existencia de interferencias externas, y por tanto cualquier cosa que se oiga en una grabación es automáticamente paranormal.

En un mundo ideal tal vez pueda ser así, que una jaula de Faraday sea capaz de eliminar cualquier interferencia electromagnética, y proteger el circuito en su interior. Sin embargo, el mundo real siempre es un poco diferente, dejando los mundos ideales como meras aproximaciones que en algunos casos pueden ser válidas, pero que en otros no lo son tanto.

Así pues, en los laboratorios secretos de Gluon con Leche, hemos construido una pequeña jaula de Faraday. Cogiendo un tetra-brik, para aprovechar la forma de caja, lo hemos envuelto con tres capas de papel de aluminio, del que todos tenemos en la cocina, y le hemos añadido una tapa de cartón, también envuelta en aluminio, y ha quedado así de bonita.

Sí, es casera, pero no por ello menos efectiva, como se verá más adelante.

Atenuación de las ondas

La física detrás de una jaula de Faraday está en las propiedades de las ondas electromagnéticas cuando se propagan en un medio conductor, como es el aluminio. En un material conductor, lo átomos que lo forman se enlazan de forma que comparten sus electrones de los orbitales más externos, y son libres de moverse por todo el material. Sin embargo, esta alta densidad de electrones libres hace que cuando una onda electromagnética intenta desplazarse por un medio así, se atenúe. Este es un matiz importante: la onda se atenúa, pero no desaparece.

Cada material posee una profundidad característica de atenuación que determina la distancia que recorre una onda hasta que su campo eléctrico se reduce en un factor 1/e=0.367 (siendo e=2.71828182845904...), es decir, cuando el campo eléctrico se reduce en un 36.7%. Nos interesa más la densidad de potencia (o cantidad de energía que atraviesa un área determinada por segundo) de una onda electromagnética, que viene dada por el cuadrado del campo eléctrico, así que en esa misma distancia, la potencia de la onda disminuye en un factor 1/e²=0.135, un 13.5%

Un 13.5% puede ser una cantidad pequeña, pero no es nula. La jaula de Faraday juega con el espesor de la paredes para que la atenuación sea la necesaria como para que la potencia que consigue atravesarla sea despeciable. Cuanto mayor sea el espesor, menos energía traspasará la jaula e interferirá con el circuito.

La profundidad característica depende además de la frecuencia de la onda incidente, de forma que una jaula puede ser efectiva para unas frecuencias, pero mala para otras. En general, cuanto mayor es la frecuencia, menor es la profundidad característica (se atenúa más rápido). He aquí una gráfica para varios conductores:

Para el aluminio, una frecuencia de 60hz necesita una pared con un espesor de alrededor de 1 cm para ser atenuada un 13%. Sin embargo, para 3 Ghz, se consigue la misma atenuación con menos de 2 micras (0.002 milímetros). De los materiales mostrados, el hierro sería el mejor de todos para hacer una jaula de Faraday, porque para el mismo espesor, atenúa más la señal que los otros materiales.

El papel de aluminio es realmente finito, aunque se le den tres vueltas. Pero para probar que nuestra jaula casera puede ejercer su función, hemos hecho lo siguiente:

Primero, hemos colocado el walkman de otras veces a unos 10 cm de un móvil, y hemos llamado. Luego hemos metido el walkman en la jaula casera, con el móvil a la misma distancia, y hemos vuelto a llamar:

Aunque no se vean en el gráfico, las interferencias también se oyen en el segundo caso, a pesar de estar atenuadas por tener que atravesar el aluminio. La frecuencia de funcionamiento de un móvil suele estar en torno a las microondas (~ 1.8 Ghz), una frecuencia que es fácilmente atenuada por el aluminio (con 5 micras de espesor, sólo pasaría un 1% de la potencia de una onda de 3 Ghz). Tres vueltas de papel de aluminio es poco, pero es probable que sean más de 5 micras. Y aún así es capaz de generar interferencias.

Hay que tener en cuenta la densidad de potencia de la onda original. Un 1% podría ser suficiente para generar interferencias. Eso sin contar con imperfecciones de la propia jaula, agujeros para pasar cables, poner botones de plástico, ventanas..., por donde se colaría parte de radiación.

Se puede llegar a una situación en que la cantidad de radiación que traspasa una jaula de Faraday es tan ínfima que se puede despreciar frente a las señales con que se va a trabajar. En otros casos, puede que no. Lo que no se puede hacer es creer de primeras que sólo por el hecho de colocar la jaula se eliminan las todas interferencias, sino que hay que comprobarlo.

Capacidades residuales

A la vista de estos espectros, ¿quién sabría decir cual fue hecho sin jaula de Faraday?

No. Esa se hizo con jaula.



Sólo la c) fue hecha sin jaula de Faraday. La a) y b) fueron hechas con la jaula, aunque con una pequeña diferencia entre ambas, que comentaremos más adelante.

Lo primero que llama la atención es cómo es posible que usando una jaula, se obtenga un resultado peor que sin usarla. Si no funcionara, lo lógico sería tener un espectro como el c), pero no que de pronto aparezcan contribuciones no esperadas.

Hay que tener en cuenta lo siguiente: tenemos un circuito, lleno de dispositivos conectados por materiales conductores, rodeado por otro conductor (la jaula), y un espacio entre medias relleno de aire, que es una material dieléctrico: eso es un condensador

El circuito tiene su propia fuente de voltaje (las pilas) y forma un circuito cerrado, mientras que la jaula no tiene referencia alguna de voltaje respecto del circuito, y con cada elemento conductor de éste va a formar un condensador. Al no tener referencia, el potencial de la jaula varía libremente, es un ruido aleatorio, que se transmite a través de estos condensadores. La capacidad e influencia que tengan depende de la geometría. Si en vez de una fluctuación aleatoria, el potencial está forzado por una interferencia externa, ésta señal se puede transmitir al circuito.

Si a alguien le da por destripar algún aparato, como el ordenador por ejemplo, en muchos de ellos encontrará una carcasa metálica, una jaula de Faraday. Y además, esta carcasa está conectada a tierra, es decir, está conectada al propio circuito del aparato en un punto concreto de referencia, de forma que mantiene un potencial definido y constante (generalmente definido como V=0) conocido respecto a cualquier otro punto del circuito. No es una solución definitiva al problema de capacidades residuales, pero sí la minimiza en gran medida.

Esto es justamente lo que falta en nuestra jaula de Faraday. Así que hemos conectado un cable al polo negativo de las pilas del walkman y el otro extremo se ha colocado haciendo contacto con el aluminio de la jaula, y entonces han desaparecido los picos de alta frecuencia, como se ve en el espectro a).

Además, hemos medido la relación señal/ruido de las frecuencias de 50hz y 150 hz:

Se han medido sin jaula, con jaula, y con la jaula conectada a tierra (al polo - de las pilas), 5 espectros de cada una para hacer la media. A 50 Hz, las barras de error son grandes y se solapan, así que no se puede asegurar que haya influencia alguna. A 150 hz sin embargo, se ve como al poner la jaula, hay una pequeña reducción de la relación señal/ruido, aunque todavía se solapan ligeramente los errores, pero cuando se conecta a tierra la relación señal/ruido cae de 13-17 a 6, es decir, la interferencia creada a 150 hz disminuye para acercarse más al nivel de ruido, y en principio, se podría pensar que es debido a minimizar el efecto de las capacidades parásitas.

Se puede ver también que la barra de error es menor siempre en el caso de la jaula conectada a tierra, lo que da idea también de mayor estabilidad en las interferencias que se crean.

Qué bonito sería el mundo y qué fácil sería todo si vivieramos en un mundo ideal. Pero no es así. El mundo ideal es la primera aproximación a la realidad, y en muchas ocasiones, es una aproximación válida. Sin embargo, es necesario saber hasta donde llega la validez de la aproximación, si nuestros instrumentos funcionan dentro de los límites de la aproximación, y qué otros fenómenos pueden darse lugar, para que cuando ocurran cosas inesperadas saber por qué han salido.