Esta entrada forma parte de una serie dedicada a la Sábana Santa. Se recomienda leer las partes precedentes a ésta.
La sábana milagrosa:
0. Introducción
1. La formación de la imagen
2. Distorsiones en 2D
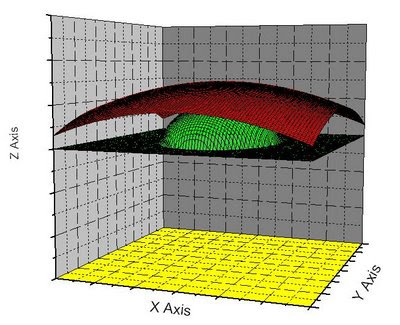
3. La representación en 3D
4. Apéndice: absorción de luz en un medio saturable
El objetivo de este apéndice es tan sólo divulgar un hecho curioso, que de rebote debería ser de aplicación en la hipótesis de la formación de la imagen en la Sábana Santa que sostienen los sindonólogos, aunque su efecto pudiera no ser muy notable. Lo leí por primera vez en la web de la NASA, donde ponen a disposición del público series de fotografías de la Luna hechas con varios módulos del programa Apollo.
Según cuentan, digitalizar las fotografías a partir de sus negativos lleva un proceso de limpieza, escaneo, y finalmente un procesado para corregir los niveles de luminosidad porque la respuesta de la película fotográfica es de tipo logarítmico, y no lineal como cualquiera pensaría de primeras. Es decir, dados dos focos de luz, donde uno tiene el doble de intensidad que el primero, en el negativo no se va a ver el doble de “oscuridad” entre un foco y otro, sino otra relación distinta, que depende de funciones logaritmo.
Al hacer una copia en papel a partir de un negativo, este tipo respuesta también está presente en el papel fotográfico, con lo que ambos procesos se cancelan, y la fotografía final sí tiene bien ajustada la luminosidad, produciendo una respuesta “lineal” entre la luz del objeto fotografiado, y su luminosidad en la fotografía final en papel.
Sin embargo, al digitalizar directamente los negativos de la misiones Apollo, la corrección debida a la respuesta de la película se tiene que hacer a posteriori, por medio de software.
¿Por qué ocurre este tipo de respuesta? Vamos a intentar explicarlo. Primero, es necesario aclarar términos, y diferenciar entre intensidad y dosis.
- Intensidad es la cantidad de fotones que cada segundo de forma continua llegan a una superficie (o que emite una fuente de luz).
- Dosis es la cantidad de total de fotones que en un determinado tiempo han llegado a una superficie (o han salido de una fuente de luz)
Son definiciones similares, pero distintas, aunque de forma informal se puede llegar a hablar de ambas como si fueran la misma cosa. Si a una superficie están llegando fotones, la intensidad dice a qué “ritmo” llegan esos fotones. La dosis dice “cuantos” fotones han llegado en total, desde que abrimos el obturador hasta que lo cerramos, sin importar el ritmo al que han llegado. La relación entre dosis e intensidad es simple: la dosis es la intensidad, multiplicada por el tiempo durante el cual los fotones han estado llegando.
A igualdad tiempo, dos intensidades distintas producen dosis distintas, pero proporcionales a las intensidades.
Dos haces de luz con distinta intensidad pueden producir la misma dosis: basta con dejar que la luz menos intensa llegue durante más tiempo, y al final en número de fotones recogidos serán el mismo. Por ejemplo, al hacer una fotografía con “poca luz”, es necesario dejar el obturador más tiempo abierto para que la fotografía final tenga suficiente claridad. Si la foto se hace con condiciones de “mucha luz”, entonces el obturador debe cerrase antes, para conseguir la misma claridad en la foto final.
Entendido esto, vayamos a ver en qué consiste una película fotográfica. Es un “papel”, o “substrato” que reacciona más o menos, según la dosis de luz que recibe. Las imágenes se componen de unidades mínimas de información, que llamamos píxeles. Un píxel por sí sólo no es una imagen, sino sólo un punto con un nivel de luminosidad determinada. Son todos los píxeles juntos con sus distintos niveles de claridad u oscuridad los que generan la imagen.
Todos tenemos una idea de lo que es un píxel en una cámara digital. En una cámara analógica, la película está compuesta de pequeños granos, que en última instancia son sus “píxeles”. Un grano no forma una imagen, sino que adquiere una luminosidad, y el conjunto de todos ellos forman la imagen
Cada uno de estos granos a su vez, tiene una gran cantidad de moléculas fotosensibles, es decir, que pueden absorber fotones, y llevar a cabo una reacción química que cambie su estructura y propiedades de forma permanente. Una vez que una molécula ha absorbido un fotón, no va a volver a absorber otro; o si lo hace, esa molécula no se va a volver “más negra”, sino que se queda como está, porque ya ha realizado la transformación que debía hacer. A efectos prácticos, una molécula reaccionada deja de estar disponible para absorber fotones.
Cuando se revela un negativo, un producto químico lo que hace es reaccionar de forma distinta con las moléculas que han sufrido este cambio por absorber un fotón, que aquellas que no lo han absorbido.

De forma que al final, cada grano contiene una concentración de moléculas con unas propiedades ópticas (digamos que “son opacas”), y de moléculas con otras propiedades ópticas distintas (“son transparentes”). Un ojo humano no es capaz de ver estas diferencias molécula a molécula, sino que de un grupo elevado de ellas, como las que hay en un grano, observa unas propiedades ópticas “promedio”, a medio camino entre la opacidad y la transparencia. Cada píxel de la imagen tiene una concentración distinta de moléculas opacas y transparentes, y el ojo ve por tanto los distintos niveles de opacidad “promedio” que forman la imagen que finalmente vemos de un negativo.

En la parte izquierda de la imagen anterior, hay distintos niveles de gris, generados a partir de los patrones indicados, que sólo contienen negro y blanco. La compresión en .jpg hace el “promedio” de ese patrón, y por eso vemos distintos niveles de grises
Otro ejemplo son las fotografías en blanco y negro de periódicos o en libros. Se puede ver como los distintos niveles de grises en realidad se deben a distintas concentraciones de puntos negros y espacios blancos.
Visto desde cierta distancia, el ojo es incapaz de ver individualmente estos puntos. Lo que vemos en esas fotografías es un “promedio” entre los puntos negros y los espacios en blanco, que el cerebro interpreta como un tono de “gris”
(Imagen de "La Pava", sacada del libro "Los caras de Bélmez", de J. Cavanilles y F. Máñez)
Así pues, uno abre el obturador, y deja que una dosis determinada de fotones llegue a la película hasta que cierra el obturador. ¿Qué nivel luminosidad tendrá un grano determinado? ¿Cuántas moléculas del grano van a reaccionar? Si tenemos N moléculas fotosensibles, y enviamos una cantidad D de fotones (menor que N), lo primero que se le ocurre a uno es que todos los fotones serán absorbidos. Y que si enviamos un número D’ (mayor que N), entonces N fotones serán absorbidos, y el resto (D’-N) pasarán de largo, o no afectarán a la película, mientras que en el negativo se obtendrá el máximo valor de gris posible (es decir, totalmente negro)
Pero veamos el proceso a cámara superlenta. Abrimos el obturador. Llega el primer fotón. Todas las moléculas están disponibles para absorber el fotón, así que el fotón tiene una probabilidad del 100% de acertar en una molécula que puede absorberlo, y hacerla reaccionar. Es absorbido, y la molécula cambia su estructura.
En seguida, llega un segundo fotón. Todas las moléculas menos una están disponibles para absorber el fotón. Da igual, como son muchas. La probabilidad de ser absorbido es del 99.9…%; otra molécula lo absorbe, y cambia su estructura.
Llega el tercero, el cuarto, el quinto… que van siendo absorbidos por moléculas que cambian su estructura. Hasta ahora, por cada fotón absorbido, hay una molécula que lo absorbe y reacciona. Pero a la vez, está disminuyendo el número de moléculas que pueden absorber un fotón. Llega un momento en que la probabilidad de ser absorbido disminuye de tal forma que el fotón no es absorbido, pasa de largo, y no genera un cambio de estructura de una molécula. De forma que la relación “un fotón-una reacción” deja de ser válida. Para cuando se cierre el obturador, si hemos dejado pasar una dosis D de fotones (menor que N), resulta que no todos los fotones se han absorbido y producido una reacción.
Coge un papel, y dibuja una tabla de 6x6 casillas. La tabla representa un píxel, o grano de la película; y cada casilla representa una molécula fotosensible. Todas las casillas están vacías, es decir, que tienes todas las moléculas disponibles para absorber fotones.
Tira un dado de seis caras dos veces. La combinación de tiradas te indica una fila y una columna. Eso indica con cual de todas las moléculas ha interaccionado el fotón que ha llegado. En la casilla de esa fila y columna, haz una cruz. Eso representa una molécula que ha reaccionado.
Haz una gráfica aparte, donde el eje x represente el número de dobles tiradas (=número de fotones que han llegado), y el eje y, el número de casillas con una cruz (=número de moléculas que han reaccionado). Al empezar, para x=0 fotones, hay y=0 moléculas reaccionadas. Tras la primera doble tirada, deberías tener x=1 fotón, e y=1 molécula. Ve marcando estos puntos. Borra la cruz en la tabla, y ahora haz dos dobles tiradas marcando las cruces correspondientes, y anota en la gráfica cuantas cruces tiene ahora la tabla (posiblemente obtendrás x=2, y=2).
Al cabo de varias repeticiones aumentando en número de tiradas, alrededor de la décima (si no antes), llegará un momento que obtengas una combinación de fila y columna que ya está marcada. Eso representa un fotón que ha encontrado una molécula que ya había reaccionado, y por tanto, ese fotón se pierde sin producir ninguna reacción.
Es posible que al inicio pensaras que si tienes 36 casillas disponibles, con 36 dobles-tiradas habrías llenado toda la tabla (“una tirada-una cruz” = “un fotón-una reacción”). Sin embargo, cuando lleves 36 tiradas, aún tendrás bastantes casillas sin marcar. Y necesitarás aún muchas más para poder llenar todas las casillas.
Si observas la gráfica que has ido construyendo, verás que tendrá más o menos esta pinta:

La curva azul representa la relación “un fotón-una reacción”. Los puntos negros representan valores que habrás ido marcando en tu gráfica. La curva roja, es la curva en torno a la cual se agrupan todos los puntos. Si repites la prueba varias veces, verás que aunque no obtengas nunca los mismos valores, los puntos siempre se agruparán en torno a esa curva.
Esta forma de simular un proceso a través de “tirar dados”, es el llamado “Método de Monte Carlo”. Procesos que pueden ser muy complejos, en los que es imposible controlar todas las variables (como saber con dónde va a caer un fotón), se simulan con un componente de azar, y se analiza el resultado global.
Es decir, no importa tanto saber cuantas moléculas habrán reaccionado tras llegar x fotones, sino la tendencia que siguen todos los valores tomados en conjunto: la línea roja.
Otro ejemplo de Método de Monte Carlo, lo usamos hace tiempo para predecir qué resultados se pueden esperar en experimentos de telepatía con cartas Zener
Cosas a destacar:
Primero, la relación entre la dosis y la “oscuridad” (o moléculas que han reaccionado) que se registra en el negativo no es “lineal”, sino del tipo “exponencial”. Si nos fijamos en la línea azul, que es la que hubiéramos esperado en principio, vemos que la curva roja se aparta de ésta. Es decir, esa curva crece más lentamente que la recta, por lo que se dice que es “sub-lineal”, lo que es típico de una función logarítmica, tal y como hablaban en la web del Apollo. (Logaritmos y exponenciales son funciones estrechamente relacionadas, así que supondremos que no quisieron ser rigurosos con el lenguaje)
Segundo, aunque un píxel tenga un determinado número de moléculas, hace falta una dosis de fotones mayor que el número de moléculas para poder hacer reaccionar todas. Y según quedan menos moléculas, se necesita una cantidad mayor de fotones para que al menos uno consiga hacer reaccionar una molécula. Es decir, el material que absorbe fotones se va poco a poco “saturando”, y la probabilidad de que un fotón sea absorbido disminuye según avanza el proceso y la saturación del material (que es lo que finalmente provoca la “sub-linealidad” del proceso)
Ahora veamos qué ocurre cuando del negativo, hacemos una copia en positivo. El proceso es prácticamente el mismo, con alguna ligera diferencia. Un foco de luz con una intensidad uniforme, ilumina un negativo. La luz lo atraviesa, pero teniendo en cuenta que el negativo presenta zonas claras (porque recibieron una dosis pequeña de fotones al hacer la foto orginal) y zonas oscuras (que recibieron una dosis más alta de fotones al hacer la fotografía), la intensidad de luz que finalmente atraviesa el negativo se modifica según este mismo patrón: de las zonas oscuras sale una dosis menor de fotones, que de la zona clara.
Cuando los fotones llegan al papel (cubierto con su propia película fotosensible), los fotones hacen lo mismo que antes: van uno a uno según llegan haciendo reaccionar las moléculas, y según la misma respuesta sub-lineal que antes. Las zonas a las que llegan pocos fotones, se vuelven claras (que corresponden a las zonas oscuras del negativo, y por tanto, a una alta intensidad de luz del objeto o escenario fotografiado), mientras que las zonas a las que llegan muchos fotones se vuelven oscuras (que correspondían a una zona clara del negativo, y por tanto a una baja intensidad de luz del objeto o escenario fotografiado)

Lo interesante resulta de comparar la intensidad de luz de la fuente de luz original, y el nivel de luminosidad de la fotografía resultante tras los dos procesos (negativo y copia): sigue una relación aproximadamente lineal entre la dosis de fotones que se capturaron al hacer la imagen, y la luminosidad que presenta la fotografía (o al menos lo hace en una zona que abarca la mayor parte de la gráfica). Esto nos asegura que la reproducción en papel tiene luminosidades “proporcionales” a la intensidad de luz del objeto o escenario real.
Mismo proceso, otra situación
La fotografía se parece a la energía nuclear de fisión lo que un huevo a una castaña. Pero lo divertido muchas veces de la física, es que situaciones que no tienen nada que ver, se pueden describir con los mismos procesos.
La fisión nuclear consiste en dividir átomos de Uranio-235 (isótopo con 92 protones, y 143 neutrones, con una abundancia del 0.07% en la naturaleza. El isótopo más abundante es el U-238). Al dividirse, libera una gran cantidad de energía que se convierte posteriormente en electricidad.
Para dividir un átomo de U235, es necesario que absorba primero un neutrón. Al hacerlo, se desestabiliza, y se divide en dos átomos más pequeños, y libera igualmente algún neutrón, que se emplea en producir otra fisión, siguiendo con la reacción en cadena.
Entonces: tenemos una barra de Uranio, que contiene un número determinado de átomos de U235. Tenemos un haz de neutrones. Un neutrón es absorbido por un átomo de U235. Éste lleva a cabo una reacción nuclear, y desaparece al fisionarse en otros dos átomos; es decir, no vuelve a estar disponible para absorber otro neutrón.
¿Cuántos átomos de Uranio235 se habrán fisionado después de que hayan llegado x neutrones? ¿Se habrán absorbido todos los neutrones enviados? ¿Cuántos átomos de U235 quedarán sin fisionar? Si aún no ves la similitud, cambia “átomo de U235” por “molécula fotosensible”, y “neutrón” por “fotón”. Las mismas relaciones matemáticas y consecuencias se aplican al caso de la fisión.
Y en este caso, es de gran importancia. Para que una reacción nuclear de fisión esté bajo control, es necesario controlar la cantidad de neutrones que llegan al Uranio. Es un equilibrio inestable que según del lado que caiga, hace que la reacción en cadena se dispare, o se frene. Afortunadamente, las centrales se diseñan para que en caso de romperse el equilibrio por cualquier motivo, la reacción se frene.
En este equilibrio entran las llamadas “barras de control”. Son unas pocas barras (generalmente de Boro) que se introducen entre las barras de Uranio. Su misión es absorber neutrones para mantener el equilibrio de la reacción en cadena.
Como hemos visto, según avanza la reacción, hay cada vez menos átomos de U235, porque desaparecen con su fisión. La probabilidad de que un neutrón sea absorbido y produzca una fisión disminuye según avanza el proceso, por lo que la reacción se puede ralentizar, y terminar parándose. Entonces, lo que se hace es ir retirando poco a poco las barras de control, para que absorban menos neutrones, y haya más disponibles para fisionar un átomo. Si hay más neutrones, hay más probabilidad de que uno de ellos sea absorbido, y produzca una fisión, manteniendo la reacción.
El ritmo al que hay que ir retirando las barras depende del ritmo al que se van fisionando los átomos, que depende del ritmo al que llegan los neutrones. Por tanto, saber cuántos Uranio U235 queda por fisionar es un dato clave para el funcionamiento de una central nuclear.
La Sábana Santa
La analogía del proceso de hacer un negativo con el de la Sábana Santa es un poco más obvio que en el caso de la fisión nuclear.
Una presunta radiación llega a la Sábana. La Sábana está compuesta por fibras de lino, cuyas moléculas absorben la radiación, y experimentan un cambio en su estructura. Según los sindonólogos, se deshidratan, es decir, pierden moléculas de agua que pudieran estar enlazadas.
Esta deshidratación cambia las propiedades ópticas de la sábana, dándole color a la imagen. Según llegan los fotones, las moléculas se van deshidratando, pero cada vez quedan menos moléculas hidratadas por deshidratar. Por lo que los fotones tienen cada vez menos probabilidad de ser absorbidos, generar una deshidratación en las moléculas, y oscurecer la tela. Nos hallamos de nuevo ante el mismo proceso.
Cuando en 1898 Secondo Pía hizo una fotografía de la Sábana Santa, observó que en el negativo aparecía la imagen más nítida, como si en realidad fuera el positivo. Eso lleva a algunos sindonólogos a hablar de la sábana como si fuera un negativo.
Si la imagen de la sábana se hubiera formado realmente como especulan los sindonólogos, sería, efectivamente, un negativo. Pero no por las razones que se esgrimen : “al invertir los colores se ve mejor la imagen”. Eso es un efecto relacionado con la percepción de la vista, que por cierto, también tiene una respuesta de tipo logarítmico, y no tiene nada que ver con el proceso de formación de la imagen.
Sería un negativo porque el proceso según el cual se habría impreso la imagen, sería el mismo por el que se genera un negativo al hacer una fotografía. Pero eso no implica nada respecto a los colores de la sábana, que la imagen se vea más nítida, y que el hombre hubiera tenido en realidad canas. Una cosa es el proceso del cerebro para la percepción de imágenes, y otra distinta el proceso físico-químico que produce una imagen en un medio saturable, ya sea en la Sábana Santa, o en un negativo fotográfico. Si se quiere hablar de la sábana como un negativo, hay que hablar de cómo se forma la imagen en ella, y no de cómo percibe el cerebro la imagen.
Conociendo entonces el proceso que hubiera seguido la sábana, hay que tener en cuenta que los niveles de luminosidad no son proporcionales a la intensidad original de la radiación, sino que es una relación “sub-lineal”. Al tratar los niveles de luminosidad de la imagen, estos deben ser corregidos teniendo en cuenta este efecto, como hemos hecho en la tercera parte, y justificamos en este apéndice.