La exploración de la Luna comenzó con un pequeño paso para un hombre, allá por Julio 1969. Y terminó en Diciembre 1972 con... un lanzamiento de martillo:
Dicen los Apoloescépticos que el hombre no ha llegado a la Luna. Que todo fue un montaje, una grabación hecha en la Tierra. Pero claro, una grabación así tiene un serio inconveniente, y es que, aunque se pueda simular el paisaje lunar y disfrazar a unos actores como astronautas, lo que no se puede simular es la gravedad lunar, que es aproximadamente un sexto de la terrestre (gT=9.81 m/s2 en la tierra, gL=1.62 m/s2 en la Luna). Así que el truco al que dicen que se recurrió fue ralentizar las imágenes.
Pero, ¿es posible simular el movimiento en una gravedad 1/6 de la terrestre sólo con ralentizar las imágenes? Pues más o menos... pero no exactamente.
Un poco de matemáticas
Supongamos que un actor disfrazado de astronauta está en un plató decorado con paisajes lunares, y para terminar su actuación, decide tirar un martillo, el cual describe un tiro parabólico. El tiro parabólico es la combinación de dos movimientos:
-Uno uniformemente acelerado en la dirección vertical sometido a la acción de la gravedad,
- Y otro rectilíneo uniforme en la dirección horizontal.
Ambos movimientos se pueden describir matemáticamente como:

El equipo de producción decide entonces ralentizar la reproducción de la grabación en un factor raíz de 6 (2.44 veces), por lo que las ecuaciones se pueden reescribir con un tiempo retardado, que vamos a llamar "tiempo lunar", tal que en un segundo lunar, el vídeo reproduce 1/2.44 segundos reales:

Matemáticamente, es indistinguible dividir el tiempo por 2.44, de dividir la gravedad entre 6 y la velocidad entre 2.44. Un espectador verá el video y creerá estar viendo tiempo real, pero como si la gravedad y la velocidad del objeto fueran menores. Entonces ralentizar un movimiento vertical sobre la Tierra en un factor raíz de 6, simularía la gravedad lunar de un objeto cuya velocidad inicial fuera además un factor raíz de 6 más lenta.
Y lo mismo ocurre en el sentido horizontal, de forma que un objeto en trayectoria parabólica sobre la Tierra (e ignorando el rozamiento con la atmósfera), al ser reproducido 2.44 veces más lento, equivaldría a un objeto en trayectoria parabólica con una velocidad 2.44 veces más lenta moviéndose en un campo gravitatorio 6 veces menor que el terrestre. Hasta aquí, de momento, parece que las matemáticas podrían dar credibilidad al argumento Apoloescéptico.
Análisis del video
En el mundo del misterio y la conspiranoia, cuando hablan de análisis de imágenes, se suelen referir a cambiar el brillo, el contraste, pasar filtros de colorines al tuntún para... bueno, normalmente para que la pareidolia haga aflorar fantasmas, poder decir cosas raras sobre pixelados, o descartar con un 99% de seguridad que no hay un fraude.
Nosotros vamos a coger el video del lanzamiento de martillo (gentileza de http://www.apolloarchive.com, sección multimedia) y vamos a hacer algo mucho menos vistoso: anotar el tiempo, y la posición en píxeles del martillo en varios fotogramas.

t_____px__py
20.64 237 98
20.84 236 81
21.04 229 71
21.92 213 40
22.16 212 37
22.32 208 33
22.56 206 32
22.72 202 29
23.04 199 29
23.12 198 28
23.28 194 29
23.48 193 31
23.60 188 32
23.80 187 33
24.16 182 40
24.60 177 50
Ahora la primera pregunta que hay que hacerse es ¿qué representan estos datos? ¿Representan posición x e y, distancia y altura? ¿Podemos compararlos directamente con una trayectoria parabólica? La respuesta es No, todavía. Nosotros somos más lentos que Santiago Camacho para esto de sacar conclusiones, y nos gusta torturar los datos primero. Que para eso somos malvados científicos escépticos comeniños amantes de la barbacoa.
Una fotografía (o un fotograma) representa en 2 dimensiones un escenario. Se pierde la información de profundidad. Por ello, no es posible conocer directamente distancias, a menos que se disponga de datos externos. Un parámetro importante de una cámara es el llamado Campo de Visión (Field Of View, FOV), que indica qué ángulo de visión ocupa la imagen. Los píxeles que hemos anotado representan la posición angular (en vertical y horizontal, o más bien, en altitud y azimut) respecto del centro de la imagen.
Dicho de otra forma, si tengo la cámara centrada apuntando a un sitio concreto, y quiero centrarla en otro punto, entonces deberé girarla hacia los lados(en horizontal, en azimut), y hacia arriba/abajo (en altitud) un ángulo determinado. Si conociera de otra forma la distancia que separa la cámara de los objetos a los que he apuntado, entonces sí que podría calcular y conocer la distancia lineal entre ellos.
El problema, sin embargo, es que estas distancias angulares las hemos tomado en unidades de "píxeles", unidad que nadie reconoce como la adecuada. Necesitamos "traducir" estos píxeles a unidades de ángulos (grados o radianes, según gustos), lo que se llama calibrar la imagen. Para ello necesitamos saber cuantos grados ocupa la imagen o parte de ella, y relacionarlo con los píxeles que ocupa. Y para ello se necesitan datos conocidos por otros métodos, como son el tamaño del módulo lunar, y la distancia de la cámara a él.
Usaremos las imágenes de la sonda Lunar Reconnaissance Orbiter (LRO), puesta en órbita en Junio de 2009. Entre sus equipos destaca la Lunar Reconnaissance Orbiter Camera (LROC) que está fotografiando la superficie de la Luna con una resolución de hasta 0.5 m/píxel. Y no han tardado en echar un vistazo a las zonas donde aterrizaron las Apollo.
EAquí tenemos la zona de Taurus-Littrow, que es donde ("presuntamente", dirían los apoloescépticos) aterrizó el módulo lunar de la Apolo 17. (La imagen original sin etiquetas es un archivo de 250 MB de peso, que se puede encontrar aquí).

En esta imagen podemos medir la distancia en píxeles desde el LRV (el Rover, el vehículo desde donde se grabaron las imágenes de forma remota) hasta el Módulo Lunar (LEM), y sabiendo que la resolución de la imagen es de 0.53 metros por píxel, llegamos a la conclusión de que entre el LRV y el LEM hay 130 metros de distancia.
Ya tenemos uno de los datos necesarios.
Para conocer el tamaño del LEM, podemos acudir a la NASA directamente.
The distance between the ends of the footpads on opposite landing legs was 9.4 m.
Entre una pata y su opuesta (en diagonal) hay 9.4 metros. Eso hace que entre las patas contiguas, la distancia sea de 9.4 divido de raíz de 2 (más o menos, 6.647 m.)
Si la distancia visible entre las patas opuestas del LEM en los fotogramas correspondiera con la diagonal entre una pata y la contraria, a 130 metros supone un ángulo de visión de 4.12º.
Pero como todo aquel que sea ligeramente perspicaz habrá notado, en el vídeo el LEM está girado respecto de esa posición, por lo que vamos a intentar afinar un poco más, aunque sabiendo ya en qué orden de magnitud nos movemos.
Podemos medir en píxeles la distancia angular entre las patas exteriores, y la pata central. Y vamos a hacer una aproximación, que es suponer que la tangente de un ángulo pequeño(en radianes) es aproximadamente igual al propio ángulo. Esta aproximación es correcta sólo cuando el ángulo considerado es pequeño, entendiendo por pequeño que el ángulo es mucho menor de un radián, y en nuestro caso, sabiendo que el máximo ángulo de visión posible es 4.12º, el error cometido en la aproximación es del orden del 1.7 por 1000 (el 0.17%)
4.12º son 0.0719 radianes, y tg(0.0719)=0.072
Así, se puede calcular que la relación que hay entre las distancias angulares entre las patas, y el ángulo en que el LEM está girado respecto a la cámara; que es 55.43º (se deja como ejercicio para el lector comprobar que la relación es correcta, yo les dejo el esquema)

Conocido el ángulo que está girado el LEM, se puede ahora calcular el ángulo real que ocupa, resultando que son 4.077º. Y sabiendo que esos 4.077º ocupan 126 píxeles de la imagen, llegamos por fin a que cada píxel representa una distancia angular de 0.03236º.
Todo este laborioso proceso (que seguramente más de uno piense que ha sido más largo que un día sin pan), ha sido sólo para calibrar la imagen, y poder relacionar unas unidades arbitrarias como son píxeles, con unidades más de "de mundo real" por decirlo de alguna manera. ¡Pero todavía tenemos que relacionarlo con distancias y alturas lineales para poder analizar un tiro parabólico!
Ya ven. Analizar o estudiar imágenes para llegar a alguna conclusión útil es algo más complicado de lo que cuentan en Cuarto Milenio y similares. Y lo que nos queda.
Si repasamos lo que hemos hecho hasta ahora, tenemos unos datos que nos indican "la dirección" en que tenemos que mirar en cada instante de tiempo. Y sabemos que nuestro astron... perdón, actor disfrazado de astronauta, está a unos 130 metros.
Ahora es cuando relacionamos las distancias angulares con el movimiento de un tiro parabólico. El movimiento temporal del azimut está relacionado con el movimiento en horizontal, y por tanto, se parece mucho a un movimiento rectilíneo uniforme, no afectado por la aceleración gravitatoria. Se parece, pero no lo es del todo. Pero eso es debido a que aún hemos de encontrar la relación entre el movimiento lineal que realiza el objeto, y el movimiento angular que queda impreso en la imagen.
Partiendo del instante inicial, tras un intervalo de tiempo t, el objeto se habrá desplazado en el plano horizontal una distancia Vx·t, siendo Vx su velocidad en el plano, y lo hará en una dirección respecto de la que está apuntando la cámara. Con un poquito de trigonometría (¡qué sería de nosotros sin ella!), podemos relacionar el ángulo de observación en azimut (ω) con la velocidad horizontal del objeto (Vx) y el ángulo de dezplazamiento respecto de la cámara (θ):


Por su parte, el movimiento temporal en altitud describe una parábola, y como cabe esperar, está relacionado con el movimento en vertical, afectado por la gravedad. Del paso anterior, sabemos ya cómo calcular la distancia horizontal que separa el objeto de la cámara, y también sabemos cómo debe comportarse el movimiento vertical; entre ambos movimientos podemos entonces saber qué ángulo de altitud debería mostrar a la cámara en cada instante de tiempo:

Y así, por fin, tenemos unas ecuacioncillas,o un modelo de cómo aparece en una cámara un movimiento parabólico, que se describe con unos parámetros clave:
- La distancia al punto inicial de lanzamiento (r0)
- El azimut inicial (ω0)
- La altitud inicial (Φ0)
- La velocidad horizontal (Vx)
- El ángulo de desplazamiento horizontal (θ)
- La velocidad inicial en vertical (Vy)
- La aceleración gravitatoria (g)
De esta forma estamos en disposición de comparar los valores "teóricos" que proporciona este modelo, con nuestros valores "experimentales" deducidos de las imágenes.
¿Y eso cómo se hace? Pues calculando los valores de los parámetros tales que el modelo reproduzca de la forma más fiel posible los datos experimentales, y posteriormente se comparan con valores conocidos de similares circunstancias.
Son varios parámetros, y varios datos, y hacerlo "a mano" es simplemente impensable. Habitualmente, los programas de tratamiento de datos poseen rutinas que hacen esta labor por nosotros, de forma que sólo hay que indicar cuales son los datos experimentales, cual es el modelo teórico, y cuales son los parámetros que debe calcular.
Tomemos nuestros datos tal cual los hemos cogido; es decir, supongamos que el tiempo transcurrido es real. El único parámetro que dejaremos fijo es la distancia inicial, que son 130 metros. El resto se calculan y el resultado es el siguiente:

Siendo los puntos los datos extraidos del vídeo, y las líneas continuas el modelo según los parámetros calculados, de los cuales resalto dos: la velocidad del objeto en horizontal (Vx=10.8±2.4 m/s), y la aceleración de la gravedad (g=1.720±0.051 m/s2).
Este valor de aceleración gravitatoria es el que hay que comparar con el valor conocido en la superficie lunar, que es 1.62 m/s2 según la wikipedia. No está mal como aproximación, entre un 3% y un 9% de diferencia, si tenemos en cuenta la incertidumbre.
Podemos repetir este mismo proceso, pero ahora dividiendo el tiempo primero entre raíz de 6. Es decir, supongamos que el tiempo medido es "tiempo lunar", y que debemos acelerarlo para recuperar la reproducción a "tiempo real" de nuestro vídeo, y entonces, descubriremos que la velocidad horizontal es de Vx=26.4±6.0 m/s (un factor 2.44 superior al cálculo anterior)... y la aceleración de la gravedad g=10.32±0.31 m/s2 , un factor 6 mayor, y entre un 2% y un 8% mayor que la real de 9.81 m/s2
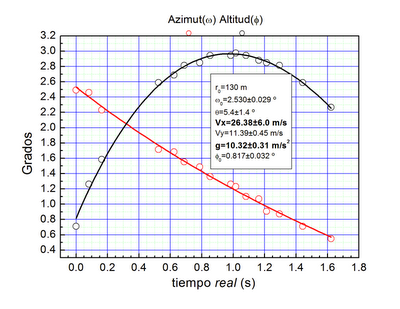
Lo cual ya sabíamos, porque las matemáticas pueden ser más o menos complicadas, pero no fallan.
¿Y la conclusión?
Bueno, pues después de maltratar y torturar los datos, es cuando hay que analizar los resultados y llegar a algún tipo de conclusión.
Lo primero, es que el movimiento es compatible con un objeto moviéndose en un campo gravitatorio lunar. Y también con un objeto moviéndose en un campo gravitatorio terrestre, cuyo tiempo de reproducción se ha modificado en el factor adecuado. Lo cual no es de mucha ayuda para los apoloescépticos, porque aunque pueda dar la razón a quien afirme que tal manipulación podría ser posible, lo cierto es que no despeja la duda sobre si el condicional habría que cambiarlo por una afirmación, y por tanto seguimos sin conclusión y con dudas.
Hay personas que les basta con tener dudas. Suele coincidir con las mismas personas que no creen que se llegara a al luna. Dudar es bueno, saludable, y aconsejable; pero el objetivo de tener dudas, es poder despejarlas para adquirir conocimiento y certezas razonables (y nótese que no digo certezas inmutables), por lo que nosotros no nos conformamos y continuamos el análisis para intentar encontrar alguna certeza razonable, si la hay.
Y seguiremos por la velocidad en horizontal. La manipulación del tiempo de reproducción modifica el tiempo (una perogrullada, sí). Como consecuencia, se modifican las velocidades y aceleración... pero no se modifican las distancias.
Por un lado hemos calculado dos velocidades, una lunar(10.8 m/s), y otra terrestre(26.4m/s).
Y por otro tenemos dos tiempos de vuelo distintos en cada caso. El máximo de altura corresponde a la mitad del tiempo de vuelo, que en el primer caso son t=2.4 x 2=4.8 segundos, y en el segundo t=0.97 x 2=1.94 s (una vez más, un factor raíz de 6)
Esto hace que la distancia recorrida tanto en un caso, como en el otro sean practicamente la misma (a pesar de que el margen de error es elevado, la diferencia entre uno y otro valor medio es del 1.2%).
d=10.8 x 4.8 =51.84 ± 11.52 metros
d=26.4 x 1.94=51.22 ± 11.64 metros
Entonces, un actor ataviado con un traje espacial, ha lanzado a una distancia de entre 40 y 62 metros, con una técnica poco ortodoxa y sin carrerilla, un martillo geológico.
No hay muchos precedentes registrados de lanzamientos de martillos geológicos, así que tendremos que comparar con lo que haya más a mano... como son las pruebas de lanzamiento en competiciones atléticas.
Echemos una vistazo a los records en la web de la IAAF.
El record del mundo de lanzamiento de martillo (siempre me he preguntado por qué lo llamán "martillo") está en 86.74 metros para hombres (conseguido en 1986). Se aleja bastante de nuestros muy optimistas 62 metros. Las mujeres no están tan lejos, 78.30 metros (2010), pero siguen por delante.
En javalina masculina nos vamos a 98.48 metros (1996), más lejos aún. En mujeres, a 72.28 metros (2008). Aunque si cogemos el record de España femenino (vía Real Federación Española de Atletismo), los 64.07 metros en 2010 estan sólo un poco por encima del límite superior del martillo geológico.
Comparemos con lanzamiento de disco: 74.08 m (1986) para hombres, 76.80 m (1988) para mujeres. En los records de España, 69.50 m (2008) en masculino sigue por encima de nuestro lanzamiento más optimista, pero el record de España femenino, 60.56 m (1994) ya es una distancia comparable.
Descartando el lanzamiento de peso (record mundial en 23.12 m en 1990), ¿qué nos queda por comparar? Pues lanzamiento de disco en Decatlón. El decatlón es una prueba combinada de carreras, saltos, y lanzamientos. Gana el que más puntos hace en función de las marcas conseguidas en cada prueba, lo que siginifica que el que gana, no tiene por qué haber hecho la mejor marca en todas las pruebas.

Así, tenemos por ejemplo que el recordman mundial de decatlón, consiguió su marca un día de 2001 que lanzó el disco a 47.79 metros, mientras que la mejor marca conseguida es de 55.87 metros en 2005. En cuanto a los españoles, el record nacional se consiguió con un lanzamiento de disco de 48.10 metros en 1998, mientras que otro decatleta consiguió en 1991 su mejor marca personal con 50.66 metros.
Como las marcas suelen variar con los años, podemos añadir como última comparación al medallista de oro de decatlón en Munich'72 (año del Apolo 17 y el lanzamiento de martillo geológico), que consiguió un lanzamiento de 46.98 metros.
Todas estas marcas de decatlón son comparables con el valor medio del lanzamiento del martillo geológico. Decíamos que la manipulación del tiempo de reproducción puede simular la gravedad lunar. Pero que no varía el espacio. Es decir, si el video se grabó en la Tierra, ¡el actor les hubiera disputado los puntos a todos estos decatletas, al menos en esta prueba!
Y hay otra cosa que no se puede simular manipulando el tiempo de reproducción, que es la capacidad, o el esfuerzo de una persona para generar el movimiento. Comparen pues, los movimientos y esfuerzo que una persona ataviada con un traje gordo, mochila, casco, y sin coger carrerilla hace al comienzo de esta entrada para lanzar un martillo geológico a más de 50 metros de distancia, con el vestuario y esfuerzo del campeón olímpico en Pekin'08 para lanzar a 53 metros el disco:
La conclusión obvia, pues, es que algunos atletas deberían cambiar su técnica de lanzamiento.
¿O era otra?

