Me gustaría vivir en el Mundodisco. Un disco plano llevado a lomos de cuatro elefantes sobre el caparazón de Gran A'tuin, una tortuga que cruza el universo sin prisa pero sin pausa, y que podría aparecer en el diagrama de Hertzsprung-Russell si le diera la gana.
La realidad es que vivo en una roca esférica achatada por los polos, que gira alrededor de una bola gigante de gas ardiendo, así que me conformo con disfrutar de obras de ficción que se desarrollan en dicho mundo.
Sin embargo, en esta roca existe gente que ¿realmente(*)? piensa que nuestro mundo es un mundo plano, aunque mucho más aburrido que el Mundodisco. Para empezar porque un muro de hielo impide contemplar el agua cayendo por el borde al vacío. De tortugas ya ni hablamos.
(*) Todavía no se si van en serio, o si son un ejemplo extremo de la Ley de Poe.
Hasta ahora, había visto este tema de reojo, sin interesarme demasiado. Tenía cierta idea preconcebida sobre las astronomía planoterrícola, pero hace poco leí a @VaryIngweion (¿Tierra plana, en serio?) y descubrí que el asunto era aún peor de lo que pensaba.
Vary comenta cómo un planoterrícola pide pruebas que él mismo pueda experimentar, porque al parecer la NASA (y la ESA, y JAXA, y los chinos, y los rusos...) son parte de una megaconspiración mundial y todas las imágenes están trucadas.
Eliminadas las pruebas obvias, la respuesta pasaría por un «¿y qué estarías dispuesto a hacer?»
Tendría que estar dispuesto a gastarse un pastón para ser un turista espacial. Las agencias espaciales acogerán con gusto un chorro de millones para subirle ahí arriba.
Más barato le podría salir montar una expedición a la Antártida para circunnavegar su costa (según ellos el límite externo del mundo) y descubrir que unos presuntos ~142.000 km de circunferencia, se quedarían en apenas ~17.000 km (a una latitud de ~ 65º Sur).
Pero como imagino que lo que quiere es algo de bajo coste, solo nos queda modelizar y observar. Un modelo es una descripción generalmente matemática del objeto de investigación, de tal forma que nos permite deducir características observables y cuantificarlas. No, con esto no va a ver directamente la curvatura de la Tierra, porque es un método indirecto. De un modelo determinado saldrán ciertos resultados; de otro modelo saldrá un resultado distinto. La observación posterior permite decidir cual de los dos modelos está más cerca de la realidad, o si el destino de ambos es la papelera.(*)
(*) Lo mínimo necesario para hacer ciencia es lápiz, papel y papelera. Si haces pseudociencia, te puedes ahorrar la papelera.
(*) que por norma general se acaba de inventar en un ataque repentino de inspiración. Ya tenemos experiencia en esas lides (1) y (2)
Así que tomaré como base lo que se detalla en la Wiki de The Flat Earth Society (TFES), sabiendo que llegará algún planoterrícola diciendo que esos solo dicen tonterías, y que su teoría es la buena de verdad.
La tentación es ponerse a argumentar todo lo que falla en Tierra plana, da para varias entradas; pero por no hacer esto muy largo, aquí va un resumen rápido de principales características, y luego me centro en la chicha necesaria para esta entrada.
La Tierra plana:
(**) La misma energía oscura postulada por malvados científicos tras detectar anomalías en la interacción gravitatoria esa que no existe.
(***) Lo cual parece la descripción de una atracción gravitatoria que no existe.
(****) Lo que no cuentan es cómo el sol puede crear el patrón de iluminación sobre la superficie que realmente se observa. (vía @haplesspete)
(*****) Variación del radio, que no de la velocidad angular, lo que es una violación de la conservación de momento angular. Me da que la energía oscura sería capaz de explicarlo.
Algunos contraargumentos al modelo de Tierra plana se pueden encontrar por aquí.
Entrando en más detalle, vamos a por los cuatro números que necesitamos.
Eratóstenes asumió que la Tierra era esférica, y el sol está tan lejos que la luz que llega a cualquier punto del planeta, llega en la misma dirección. Si en un punto dado observamos que la luz incide con otro ángulo, es porque la superficie de la Tierra se ha curvado. Hay una relación clara entre el ángulo de incidencia de la luz y la curvatura, por lo que se puede estimar la circunferencia total (y deducir el radio o diámetro del globo).
Si entre dos puntos a 926 km hay un ángulo de 7º12', la fracción de 7º12' respecto a una vuelta entera (360º) es la misma fracción que entre 926 km respecto a la circunferencia total, resultando 46.300 km, que como primera aproximación no está mal. Teniendo en cuenta que la Tierra no es exactamente esférica, Eratóstenes sobrestimó el radio medio de la Tierra en un 15%.
Sin embargo, en una Tierra plana con un sol más cercano, la inclinación con que llega la luz es debida a la posición del sol. Es otra interpretación, otro modelo, que lleva obviamente a otras conclusiones.
Pero aquí nos topamos con una trampa de TFES: La distancia del Polo Norte al Sur abarca latitudes(*) desde +90º a -90º (en total: 180º), así que la relación de 7º12' a 180º es la misma que hay entre 926 km y el radio: R=23.150 km, lo que nos da un Diámetro=2·R=46.300 km.
(*) Usar una variable como la Latitud implica estar usando coordenadas esféricas. No parece lo más apropiado si lo que se pretende es negar precisamente la esfericidad de la Tierra.
¡Oh, qué curioso!¡Nos sale el mismo número!
No tan curioso, porque lo que han hecho son las mismas cuentas que Eratóstenes para una Tierra esférica (por eso sale el mismo resultado), pero dicen que el resultado es otra cosa; porque ellos lo valen. Han operado números sin darles ningún sentido, cual piramidólogo aficionado.
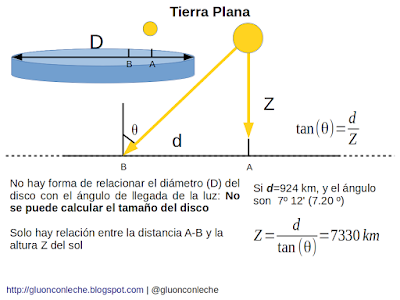
El problema es que en un modelo de Tierra plana no existe ninguna relación entre el tamaño del disco y el ángulo con que incide la luz del sol. El disco podría ser más largo, o más corto, y no afectaría al ángulo con el que llegaría la luz en esos puntos, siempre que la altura del sol sea la misma, porque eso es lo que realmente se puede calcular con los datos disponibles: la altura del sol sobre Tierra plana sería de 7330 km.
O no.
Según TFES, el sol [de 32 millas de tamaño] gira a una altura de 3000 millas, que (suponiendo en el mejor de los casos que sean millas náuticas) son 5556 km. Demostrando así que en TFES ni se han molestado en encender la calculadora(*). Por otro lado, he podido encontrar algún video de youtube donde hablan de una altura de 7.000 km, aunque no dice de donde saca el valor.
(*) o que hace falta que incluir el efecto de la energía oscura.
Esta es la razón por la que las pseudociencias en general nunca concretan: porque se detecta en seguida que los datos son inventados. Aún así, a pesar de que el cálculo del radio planoterrícola no tiene sentido, es el dato con el que vamos a seguir adelante; y consideraré las dos presuntas alturas del sol de 5556 km y 7330 km.(*)
(*) Si algún planoterrícola ha llegado hasta aquí, es posible que estédespotricando en desacuerdo. Le agradecería que me diera los valores que él considera correctos (y de donde salen, claro)
La propia TFES dice que:
El movimiento del sol es un ejemplo que nos dice que no vivimos en un mundo esférico heliocéntrico.
Pues vamos a comprobarlo. Porque según se deduce del modelo de la Tierra plana, el sol NUNCA bajará por el horizonte. En su giro alrededor del eje del Polo Norte, cuando se acerque a nosotros el sol se elevará en el cielo; al alejarse bajará, pero nunca pasará por debajo del horizonte. Según los planoterrícolas, el sol simplemente se aleja (acerca, en el amanecer), y en el momento que aparentemente roza el horizonte, la desaparición (aparición) es solo una cuestión de perspectiva, un efecto óptico.
En cambio, en una Tierra esférica el sol pasará por debajo del horizonte, para subir de nuevo por el lado contrario.
A priori alguien puede pensar que ambas descripciones cualitativas podrían ser equivalentes, y son solo interpretaciones distintas del mismo fenómeno. Pero la potencia de un modelo es poder poner números a estas descripciones, y hacerlas cuantitativas. Son movimientos lo suficientemente distintos como para distinguir cuantitativamente (a través de experimentos u observaciones) entre ambos modelos.
Lo primero que necesitamos es saber nuestra posición en el disco. Para lo cual tiramos de nuevo de TFES y descubrimos que nuestra posición se puede describir en latitud y longitud (*) tal que así:
(*) Sí, de nuevo coordenadas esféricas en un disco plano
Así que, yo por ejemplo, estoy en torno a ~40º N, ~3º O, tanto en la Tierra esférica como en Tierra plana. Pero en Tierra plana lo que necesito realmente es mi distancia respecto al centro, el Polo Norte. Usando la misma matemática planoterrícola, si de 90º a -90º hay 23.150 km, desde el Polo Norte a mi posición hay 6.398 km.(*)
También necesito el radio de la circunferencia que describe el sol sobre la superficie. Durante los equinoccios, el sol está sobre el ecuador, a la mitad del radio. El sol gira trazando circunferencias con un radio de 11.575 km.(**)
Durante los solsticios, en verano (trópico de Cáncer, 23º26'14'' N) gira a 8.561 km del Polo Norte, y en invierno (trópico de Capricornio, 23º26'14'' S) a 14.589 km. (***)
(*) podría calcular esa misma distancia según una Tierra esférica, para descubrir que es del orden de ~5.500 km. Pero claro, es matemática globoterrícola, faltaría la corrección por acción de la energía oscura.
(**) ~10.000 km globoterrícolas.
(***) ~7.400 km, y ~12.600 km globoterrícolas, respectivamente.
Sabiendo que la altura del sol es 5556 km (o alternativamente, 7330 km) sobre la superficie, la simple trigonometría nos permite calcular a qué altura sobre el horizonte se observará el sol a cualquier hora del día en estos tres casos desde mi punto de observación.
No mucho más complejas son las ecuaciones para calcular la altura del sol sobre el horizonte en una Tierra esférica, conocidas la declinación y ascensión recta en un día determinado.
Veamos:
Efectivamente, en una Tierra plana al atardecer el sol baja hacia el horizonte, ¡pero no lo roza ni de lejos, no baja más de 15~20º en el mejor de los casos!. Mientras, en una Tierra esférica, el sol pasa por debajo del horizonte.
Y en general podemos ver que hay una enorme diferencia entre el movimiento del sol en una Tierra plana frente a una esférica. ¡Perfecto! Justo lo que necesitamos para poder hacer unas medidas, y comprobar que, como mínimo, uno de los dos modelos es erróneo.(*)
(*) Un lector avispado observará cómo en el punto más alto durante los equinoccios, el modelo de Tierra esférica predice que en mi posición la luz del sol llegaría a unos ~50º sobre el horizonte. Que se traduce en 90-50=40º respecto de la vertical, coincidiendo con la latitud del lugar. Recordemos que esa es precisamente la definición de latitud; pero el modelo de Tierra plana no es capaz de reproducir tal definición. Es lo que tiene inventarse las cosas, que luego no encajan ni a martillazos.
¿Y cómo medimos la altura del sol sobre el horizonte? ¿Qué tipo de instrumentación avanzada necesitamos? ¿Estará dentro de nuestras posibilidades económicas?
Átese el hilo a un objeto pesado, y cuélguese de borde superior del transportador de ángulos. Añádase un par de cartones con agujeros a modo de «mirillas». Ahora, podemos mirar a través de las mirillas hacia el objeto de interés (generalmente, un astro), y la plomada marcará el ángulo que hemos tenido que girar el artilugio.
Preguntaba al principio al potencial lector planoterrícola «¿qué estarías dispuesto a hacer?». Espero que entre esas cosas esté madrugar un poco, irte con un cuadrante, y emplear un día entero midiendo la altura del sol. Búscate un sitio con buena visión del horizonte, sin montañas, colinas, casas,... al menos para el amanecer y atardecer. Luego, es sol se ve desde cualquier parte. No es imprescindible medir en un sitio fijo, puedes moverte al pueblo de al lado sin problema. Pero tampoco salgas de viaje y midas en Badajoz por la mañana, y en Barcelona por la tarde.
Una observación cada hora es suficiente. No hace falta que sea estricto, pero intenta abarcar el día completo mientras el sol esté visible.
Yo ya lo hice. Un 22 de Julio, con un sol a ~20º de declinación y ~8h10' de Ascensión Recta(*). Hasta que se nubló. Y que leches, era verano y me fui a por una muy merecida cerveza.
(*) En Tierra plana, el sol describiría circunferencias de 9003 km de radio
Y mis conclusiones son que:
Será que los fabricantes de transportadores de ángulos están en la conspiración. O que no he tenido en cuenta la energía oscura. O que las leyes de la óptica tampoco son como nos han contado hasta ahora, para desgracia de Maxwell. O todo a la vez. Algún buen pseudocientífico ya se inventará una explicación «ad hoc», un parche más.
Porque tú lo que realmente quieres es ver directamente con tus ojos la curvatura de la Tierra. Para tí, los senos y thetas son otra cosa, no engañabobos de la ciencia oficial. Si así piensas, entonces sólo me queda aconsejarte que vayas ahorrando dinero para que alguna agencia espacial te lleve algún día de turista espacial.
Más no puedo hacer.
O no estoy dispuesto a hacer.
En la wiki de TFES, definen «Flat-Earther» como «aquel que cree en la teoría de la Tierra plana». Yo, sin embargo, no creo en una Tierra esférica.
Porque no hace falta creer en lo que existe.
El Mundodisco, por muy imaginario que sea, tiene su gracia. Tiene incluso una coherencia interna dentro de su lógica fantástica... pero, ¿la Tierra plana? Venga, no jodas (disculpen mi klatchiano).
La realidad es que vivo en una roca esférica achatada por los polos, que gira alrededor de una bola gigante de gas ardiendo, así que me conformo con disfrutar de obras de ficción que se desarrollan en dicho mundo.
Sin embargo, en esta roca existe gente que ¿realmente(*)? piensa que nuestro mundo es un mundo plano, aunque mucho más aburrido que el Mundodisco. Para empezar porque un muro de hielo impide contemplar el agua cayendo por el borde al vacío. De tortugas ya ni hablamos.
(*) Todavía no se si van en serio, o si son un ejemplo extremo de la Ley de Poe.
Hasta ahora, había visto este tema de reojo, sin interesarme demasiado. Tenía cierta idea preconcebida sobre las astronomía planoterrícola, pero hace poco leí a @VaryIngweion (¿Tierra plana, en serio?) y descubrí que el asunto era aún peor de lo que pensaba.
Vary comenta cómo un planoterrícola pide pruebas que él mismo pueda experimentar, porque al parecer la NASA (y la ESA, y JAXA, y los chinos, y los rusos...) son parte de una megaconspiración mundial y todas las imágenes están trucadas.
Eliminadas las pruebas obvias, la respuesta pasaría por un «¿y qué estarías dispuesto a hacer?»
Tendría que estar dispuesto a gastarse un pastón para ser un turista espacial. Las agencias espaciales acogerán con gusto un chorro de millones para subirle ahí arriba.
Más barato le podría salir montar una expedición a la Antártida para circunnavegar su costa (según ellos el límite externo del mundo) y descubrir que unos presuntos ~142.000 km de circunferencia, se quedarían en apenas ~17.000 km (a una latitud de ~ 65º Sur).
Pero como imagino que lo que quiere es algo de bajo coste, solo nos queda modelizar y observar. Un modelo es una descripción generalmente matemática del objeto de investigación, de tal forma que nos permite deducir características observables y cuantificarlas. No, con esto no va a ver directamente la curvatura de la Tierra, porque es un método indirecto. De un modelo determinado saldrán ciertos resultados; de otro modelo saldrá un resultado distinto. La observación posterior permite decidir cual de los dos modelos está más cerca de la realidad, o si el destino de ambos es la papelera.(*)
(*) Lo mínimo necesario para hacer ciencia es lápiz, papel y papelera. Si haces pseudociencia, te puedes ahorrar la papelera.
La Tierra Plana
Pero una vez en harina, resulta muy complicado tener un modelo de una Tierra plana como Offler manda. Simplemente, porque como toda pseudociencia que se precie, solo hace vagas descripciones sin chicha suficiente como para poder compararlas con la realidad. Lo importante se deja en el aire para que cuando un malvado escéptico comeniños (y globoterrícola) ponga los cuatro números necesarios, y demuestre que cualquier parecido con la realidad es pura coincidencia, el planoterrícola de turno diga que está mal porque hace falta una nueva hipótesis «ad hoc»(*)(*) que por norma general se acaba de inventar en un ataque repentino de inspiración. Ya tenemos experiencia en esas lides (1) y (2)
Así que tomaré como base lo que se detalla en la Wiki de The Flat Earth Society (TFES), sabiendo que llegará algún planoterrícola diciendo que esos solo dicen tonterías, y que su teoría es la buena de verdad.
La tentación es ponerse a argumentar todo lo que falla en Tierra plana, da para varias entradas; pero por no hacer esto muy largo, aquí va un resumen rápido de principales características, y luego me centro en la chicha necesaria para esta entrada.
La Tierra plana:
- tiene forma de disco, y en su centro está el Polo Norte. El Polo Sur no es un punto, sino que la Antártida es un muro de hielo gigante en el borde del disco, que evita que el agua se caiga. Más allá del muro, unos dicen que el hielo se extiende hasta el infinito, y otros que ahí termina el disco.
- No existe la gravedad, sino una aceleración constante equivalente. Lo dijo Einstein, oiga(*). Y esa la aceleración la provoca la energía oscura del universo(**).
- El disco está quieto, no gira. Las borrascas y anticiclones no son creadas por fuerzas de Coriolis, sino por fuerzas de atracción de otros sistemas celestes(***).
- El Sol no es una bola gigante a mucha distancia, sino una bolita más discreta y mucho más cerca, que gira sobre la Tierra plana, iluminando sólo una parte del disco creando así los días y noches.(****)
- Además, el Sol cambia el radio de su giro desde un trópico hasta el otro, pasando por el ecuador, creando así las estaciones(*****).
(**) La misma energía oscura postulada por malvados científicos tras detectar anomalías en la interacción gravitatoria esa que no existe.
(***) Lo cual parece la descripción de una atracción gravitatoria que no existe.
(****) Lo que no cuentan es cómo el sol puede crear el patrón de iluminación sobre la superficie que realmente se observa. (vía @haplesspete)
(*****) Variación del radio, que no de la velocidad angular, lo que es una violación de la conservación de momento angular. Me da que la energía oscura sería capaz de explicarlo.
Algunos contraargumentos al modelo de Tierra plana se pueden encontrar por aquí.
Entrando en más detalle, vamos a por los cuatro números que necesitamos.
¿Cuánto mide el disco terráqueo?
Según TFES, 25.000 millas náuticas de diámetro (que son 46.300 Km de diámetro, o un radio de 23.150 km). ¿Cómo llegan a este resultado? Pues gracias a Eratóstenes. Sí, el mismo que estimó la circunferencia de la esfera terrestre.Eratóstenes asumió que la Tierra era esférica, y el sol está tan lejos que la luz que llega a cualquier punto del planeta, llega en la misma dirección. Si en un punto dado observamos que la luz incide con otro ángulo, es porque la superficie de la Tierra se ha curvado. Hay una relación clara entre el ángulo de incidencia de la luz y la curvatura, por lo que se puede estimar la circunferencia total (y deducir el radio o diámetro del globo).
Si entre dos puntos a 926 km hay un ángulo de 7º12', la fracción de 7º12' respecto a una vuelta entera (360º) es la misma fracción que entre 926 km respecto a la circunferencia total, resultando 46.300 km, que como primera aproximación no está mal. Teniendo en cuenta que la Tierra no es exactamente esférica, Eratóstenes sobrestimó el radio medio de la Tierra en un 15%.
Sin embargo, en una Tierra plana con un sol más cercano, la inclinación con que llega la luz es debida a la posición del sol. Es otra interpretación, otro modelo, que lleva obviamente a otras conclusiones.
Pero aquí nos topamos con una trampa de TFES: La distancia del Polo Norte al Sur abarca latitudes(*) desde +90º a -90º (en total: 180º), así que la relación de 7º12' a 180º es la misma que hay entre 926 km y el radio: R=23.150 km, lo que nos da un Diámetro=2·R=46.300 km.
(*) Usar una variable como la Latitud implica estar usando coordenadas esféricas. No parece lo más apropiado si lo que se pretende es negar precisamente la esfericidad de la Tierra.
¡Oh, qué curioso!¡Nos sale el mismo número!
No tan curioso, porque lo que han hecho son las mismas cuentas que Eratóstenes para una Tierra esférica (por eso sale el mismo resultado), pero dicen que el resultado es otra cosa; porque ellos lo valen. Han operado números sin darles ningún sentido, cual piramidólogo aficionado.
El problema es que en un modelo de Tierra plana no existe ninguna relación entre el tamaño del disco y el ángulo con que incide la luz del sol. El disco podría ser más largo, o más corto, y no afectaría al ángulo con el que llegaría la luz en esos puntos, siempre que la altura del sol sea la misma, porque eso es lo que realmente se puede calcular con los datos disponibles: la altura del sol sobre Tierra plana sería de 7330 km.
O no.
Según TFES, el sol [de 32 millas de tamaño] gira a una altura de 3000 millas, que (suponiendo en el mejor de los casos que sean millas náuticas) son 5556 km. Demostrando así que en TFES ni se han molestado en encender la calculadora(*). Por otro lado, he podido encontrar algún video de youtube donde hablan de una altura de 7.000 km, aunque no dice de donde saca el valor.
(*) o que hace falta que incluir el efecto de la energía oscura.
Esta es la razón por la que las pseudociencias en general nunca concretan: porque se detecta en seguida que los datos son inventados. Aún así, a pesar de que el cálculo del radio planoterrícola no tiene sentido, es el dato con el que vamos a seguir adelante; y consideraré las dos presuntas alturas del sol de 5556 km y 7330 km.(*)
(*) Si algún planoterrícola ha llegado hasta aquí, es posible que esté
Un experimento bueno, bonito y barato
Había alguien que quería hacer un experimento para comprobar por sí mismo que la Tierra es esférica. Descartados los métodos directos (unos por conspiranoia, otros por caros), yo lo que le propongo es hacer una observación experimental, y comprobar qué modelo se ajusta mejor a los datos: si una Tierra plana o una Tierra esférica.La propia TFES dice que:
The world looks flat, the bottoms of clouds are flat, the movement of the sun; these are all examples of your senses telling you that we do not live on a spherical heliocentric world(énfasis mío)
El movimiento del sol es un ejemplo que nos dice que no vivimos en un mundo esférico heliocéntrico.
Pues vamos a comprobarlo. Porque según se deduce del modelo de la Tierra plana, el sol NUNCA bajará por el horizonte. En su giro alrededor del eje del Polo Norte, cuando se acerque a nosotros el sol se elevará en el cielo; al alejarse bajará, pero nunca pasará por debajo del horizonte. Según los planoterrícolas, el sol simplemente se aleja (acerca, en el amanecer), y en el momento que aparentemente roza el horizonte, la desaparición (aparición) es solo una cuestión de perspectiva, un efecto óptico.
En cambio, en una Tierra esférica el sol pasará por debajo del horizonte, para subir de nuevo por el lado contrario.
A priori alguien puede pensar que ambas descripciones cualitativas podrían ser equivalentes, y son solo interpretaciones distintas del mismo fenómeno. Pero la potencia de un modelo es poder poner números a estas descripciones, y hacerlas cuantitativas. Son movimientos lo suficientemente distintos como para distinguir cuantitativamente (a través de experimentos u observaciones) entre ambos modelos.
Lo primero que necesitamos es saber nuestra posición en el disco. Para lo cual tiramos de nuevo de TFES y descubrimos que nuestra posición se puede describir en latitud y longitud (*) tal que así:
(*) Sí, de nuevo coordenadas esféricas en un disco plano
- Longitud: Sabiendo las horas de diferencia del mediodía solar respecto a Greenwich [y multiplicando por 15º/hora, añado yo]
- Latitud: corresponde con el ángulo de inclinación de los rayos solares respecto de la vertical, el día del equinoccio, en su punto más alto [es decir, al mediodía solar].
Así que, yo por ejemplo, estoy en torno a ~40º N, ~3º O, tanto en la Tierra esférica como en Tierra plana. Pero en Tierra plana lo que necesito realmente es mi distancia respecto al centro, el Polo Norte. Usando la misma matemática planoterrícola, si de 90º a -90º hay 23.150 km, desde el Polo Norte a mi posición hay 6.398 km.(*)
También necesito el radio de la circunferencia que describe el sol sobre la superficie. Durante los equinoccios, el sol está sobre el ecuador, a la mitad del radio. El sol gira trazando circunferencias con un radio de 11.575 km.(**)
Durante los solsticios, en verano (trópico de Cáncer, 23º26'14'' N) gira a 8.561 km del Polo Norte, y en invierno (trópico de Capricornio, 23º26'14'' S) a 14.589 km. (***)
(*) podría calcular esa misma distancia según una Tierra esférica, para descubrir que es del orden de ~5.500 km. Pero claro, es matemática globoterrícola, faltaría la corrección por acción de la energía oscura.
(**) ~10.000 km globoterrícolas.
(***) ~7.400 km, y ~12.600 km globoterrícolas, respectivamente.
Sabiendo que la altura del sol es 5556 km (o alternativamente, 7330 km) sobre la superficie, la simple trigonometría nos permite calcular a qué altura sobre el horizonte se observará el sol a cualquier hora del día en estos tres casos desde mi punto de observación.
No mucho más complejas son las ecuaciones para calcular la altura del sol sobre el horizonte en una Tierra esférica, conocidas la declinación y ascensión recta en un día determinado.
Veamos:
Efectivamente, en una Tierra plana al atardecer el sol baja hacia el horizonte, ¡pero no lo roza ni de lejos, no baja más de 15~20º en el mejor de los casos!. Mientras, en una Tierra esférica, el sol pasa por debajo del horizonte.
Y en general podemos ver que hay una enorme diferencia entre el movimiento del sol en una Tierra plana frente a una esférica. ¡Perfecto! Justo lo que necesitamos para poder hacer unas medidas, y comprobar que, como mínimo, uno de los dos modelos es erróneo.(*)
(*) Un lector avispado observará cómo en el punto más alto durante los equinoccios, el modelo de Tierra esférica predice que en mi posición la luz del sol llegaría a unos ~50º sobre el horizonte. Que se traduce en 90-50=40º respecto de la vertical, coincidiendo con la latitud del lugar. Recordemos que esa es precisamente la definición de latitud; pero el modelo de Tierra plana no es capaz de reproducir tal definición. Es lo que tiene inventarse las cosas, que luego no encajan ni a martillazos.
¿Y cómo medimos la altura del sol sobre el horizonte? ¿Qué tipo de instrumentación avanzada necesitamos? ¿Estará dentro de nuestras posibilidades económicas?
El cuadrante
Por el módico precio de un eurillo de nada, podemos comprar un transportador de ángulos, buscar un hilo y algo pesado, para construir un instrumento conocido y utilizado satisfactoriamente desde hace siglos: un cuadrante.Átese el hilo a un objeto pesado, y cuélguese de borde superior del transportador de ángulos. Añádase un par de cartones con agujeros a modo de «mirillas». Ahora, podemos mirar a través de las mirillas hacia el objeto de interés (generalmente, un astro), y la plomada marcará el ángulo que hemos tenido que girar el artilugio.
NOTA IMPORTANTE: Mirar directamente al sol es perjudicial para los ojos. Para apuntar al sol sin hacerse daño en la vista, es mejor proyectar la luz que pasa por la primera mirilla, y observar en la segunda dónde cae el punto de luz. Cuando esté centrado en la segunda mirilla, estaremos apuntando correctamente al sol.
Medidas reales
~7h de la mañana (5h UTC), y un solazo asciende desde el horizonte.
Preguntaba al principio al potencial lector planoterrícola «¿qué estarías dispuesto a hacer?». Espero que entre esas cosas esté madrugar un poco, irte con un cuadrante, y emplear un día entero midiendo la altura del sol. Búscate un sitio con buena visión del horizonte, sin montañas, colinas, casas,... al menos para el amanecer y atardecer. Luego, es sol se ve desde cualquier parte. No es imprescindible medir en un sitio fijo, puedes moverte al pueblo de al lado sin problema. Pero tampoco salgas de viaje y midas en Badajoz por la mañana, y en Barcelona por la tarde.
Una observación cada hora es suficiente. No hace falta que sea estricto, pero intenta abarcar el día completo mientras el sol esté visible.
~8h de la mañana (6h UTC), y el cuadrante me marca unos imposibles 8º grados en una Tierra plana. Esto no hay perspectiva que lo arregle.
Yo ya lo hice. Un 22 de Julio, con un sol a ~20º de declinación y ~8h10' de Ascensión Recta(*). Hasta que se nubló. Y que leches, era verano y me fui a por una muy merecida cerveza.
(*) En Tierra plana, el sol describiría circunferencias de 9003 km de radio
Y mis conclusiones son que:
- Las observaciones no coinciden con el modelo de Tierra plana. No es capaz de reproducir la realidad.
- El modelo de Tierra plana ni siquiera tiene coherencia interna, porque no es capaz de reproducir ni definiciones elementales (como la de latitud).
- El modelo de Tierra esférica sí reproduce las observaciones experimentales. De momento, falso no es.
Será que los fabricantes de transportadores de ángulos están en la conspiración. O que no he tenido en cuenta la energía oscura. O que las leyes de la óptica tampoco son como nos han contado hasta ahora, para desgracia de Maxwell. O todo a la vez. Algún buen pseudocientífico ya se inventará una explicación «ad hoc», un parche más.
Porque tú lo que realmente quieres es ver directamente con tus ojos la curvatura de la Tierra. Para tí, los senos y thetas son otra cosa, no engañabobos de la ciencia oficial. Si así piensas, entonces sólo me queda aconsejarte que vayas ahorrando dinero para que alguna agencia espacial te lleve algún día de turista espacial.
Más no puedo hacer.
O no estoy dispuesto a hacer.
¿Quién cree en las puertas?
Didáctilos, un filósofo de Efebia, hablaba de cómo la gente cree en diversos dioses, pero nadie cree en las puertas.En la wiki de TFES, definen «Flat-Earther» como «aquel que cree en la teoría de la Tierra plana». Yo, sin embargo, no creo en una Tierra esférica.
Porque no hace falta creer en lo que existe.
El Mundodisco, por muy imaginario que sea, tiene su gracia. Tiene incluso una coherencia interna dentro de su lógica fantástica... pero, ¿la Tierra plana? Venga, no jodas (disculpen mi klatchiano).