(bonito pueblo por cierto, que no necesitaría el reclamo del hombre pez para atraer turistas)
Esta entrada forma parte de una serie dedicada a la Sábana Santa. Se recomienda leer las partes precedentes a ésta.
La sábana milagrosa:
0. Introducción
1. La formación de la imagen
2. Distorsiones en 2D
3. La representación en 3D
4. Apéndice: absorción de luz en un medio saturable
En la parte izquierda de la imagen anterior, hay distintos niveles de gris, generados a partir de los patrones indicados, que sólo contienen negro y blanco. La compresión en .jpg hace el “promedio” de ese patrón, y por eso vemos distintos niveles de grises
Otro ejemplo son las fotografías en blanco y negro de periódicos o en libros. Se puede ver como los distintos niveles de grises en realidad se deben a distintas concentraciones de puntos negros y espacios blancos.
Visto desde cierta distancia, el ojo es incapaz de ver individualmente estos puntos. Lo que vemos en esas fotografías es un “promedio” entre los puntos negros y los espacios en blanco, que el cerebro interpreta como un tono de “gris”
(Imagen de "La Pava", sacada del libro "Los caras de Bélmez", de J. Cavanilles y F. Máñez)
Esta forma de simular un proceso a través de “tirar dados”, es el llamado “Método de Monte Carlo”. Procesos que pueden ser muy complejos, en los que es imposible controlar todas las variables (como saber con dónde va a caer un fotón), se simulan con un componente de azar, y se analiza el resultado global.
Es decir, no importa tanto saber cuantas moléculas habrán reaccionado tras llegar x fotones, sino la tendencia que siguen todos los valores tomados en conjunto: la línea roja.
Otro ejemplo de Método de Monte Carlo, lo usamos hace tiempo para predecir qué resultados se pueden esperar en experimentos de telepatía con cartas Zener
Esta entrada forma parte de una serie dedicada a la Sábana Santa. Se recomienda leer las partes precedentes a ésta.
La sábana milagrosa:
0. Introducción
1. La formación de la imagen
2. Distorsiones en 2D
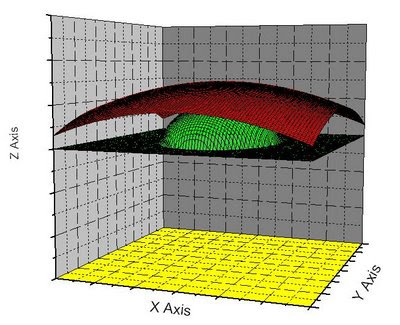
3. La representación en 3D
4. Apéndice: absorción de luz en un medio saturable
Un cambio del 10 % en el nivel de intensidad entrante, produce un cambio en la elevación del 10% en el eje Z. Es una función directa, lineal.
Este trabalenguas se puede resumir en una gráfica: si en el eje horizontal ponemos los niveles de grises, y en el eje vertical la altura z que le corresponde, la gráfica que resulta es una recta:
Si nos fijamos en la recta morada, por cada dos cuadritos que se avanza en horizontal, se sube uno en vertical. Si en vez de 2, avanzamos 4 cuadritos en horizontal (el doble), entonces en vertical en vez de uno, son dos cuadritos (también el doble) lo que asciende la recta. En ambos casos la relación entre la altura ascendida, y la distancia en horizontal es la misma, y ese valor se denomina constante de proporcionalidad
Entonces, proporcionalidad (o linealidad) significa que las variables se relacionan por una recta. El parámetro a es la constante de proporcionalidad, que establece cual es esa “proporción”, es decir: “cómo de empinada” es la recta. El parámetro b no afecta a la proporción (“no afecta a la pendiente de la recta”). Por eso el primer parámetro es el importante, mientras que el segundo se puede ignorar la mayoría de las veces. Dos rectas con el parámetro a idéntico, pero distinto valor de b, representan la misma relación de proporcionalidad.
Bueno, ya conocemos (y entendemos, o eso espero) un dato importante: el VP-8 relaciona el nivel de gris y altura a través de una recta. Pero, ¿qué recta exactamente? Existen infinitas rectas, pero sólo una debería ser la correcta. Cuando se desarrolla una hipótesis para relacionar dos variables de forma proporcional, primero se deduce (o se asume justificando por qué) que tal relación es una recta. Luego, se calcula la constante de proporcionalidad a. Finalmente, se hace un experimento para comprobar:
1- Que las variables se relacionan a través de una recta
2- Que la proporción coincide con la calculada
Si el resultado es una recta, hemos demostrado que la mitad de la hipótesis es correcta, y la teoría va por buen camino. Si además coincide (dentro del margen de error) con la proporción, la hipótesis ha pasado todo el test. Si no, habrá que volver atrás y modificar algún punto de la teoría para calcular de nuevo el parámetro a, sin desechar la hipótesis aún. Pero si la gráfica ni siquiera es una recta, entonces habrá que hacer uso de la papelera, empezar desde el principio, y suponer otro tipo de relación no proporcional.
¿Qué ocurre en el caso de la Sábana Santa? Que no sabemos cómo se relacionan los valores de intensidad y altura. JJS metieron la imagen en el analizador. El analizador formó una imagen 3D basándose en sus propias reglas de proporcionalidad, y los tres creyeron entonces que la intensidad de la imagen se relacionaba con la altura o topografía del cuerpo.
Es decir, hicieron una observación experimental, pero no existe ninguna razón para pensar que esa observación deba de ser correcta, ni nadie ha comprobado si esa observación tiene que ser correcta. Simplemente, se ha asumido sin más. La relación entre intensidad y altura no tiene por qué ser lineal. Y si lo fuera, no sabemos qué parámetros de la recta son los correctos para hacer la comparación. Tanto el VP-8, como la mayoría de programas actuales y más modernos que representan en pseudo3D, pueden variar arbitrariamente la constante de proporcionalidad: tienen un “botón” que modifica la pendiente de esa recta. Y se puede modificar hasta conseguir que la imagen aparente estar bien proporcionada: que el tamaño de la nariz en vertical esté proporcionado con respecto al tamaño de la cabeza, por ejemplo.
Dos imágenes cambiando los parámetros de la recta que relaciona altura con intensidad: no todos los valores dan lugar a una imagen que parezca coherente con el volumen de un cuerpo en 3D.
Esos parámetros podrían dar información que seria relevante, por ejemplo, para entender la naturaleza de la presunta radiación, pero sin hipótesis, no dejan de ser unos simples números sin sentido.
Esto legitima a emplear idéntica arbitrariedad a cualquier otra imagen para demostrar que un dibujo también puede presentarse en pseudo3D con unas proporciones aparentemente aceptables, pudiendo refutar así el argumento de que la tridimensionalidad de la Sábana Santa es un fenómeno único, y no reproducible de cualquier otra forma, en ningún tipo de fotografía, imagen, dibujo, etc….
Cuando se activó el modo de imagen pseudo-tridimensional, una imagen “tridimensional verdadera” apareció en el monitor. Al menos, había suficientes trazas de una estructura tridimensional real en la imagen mostrada. La nariz hacía rampa en relieve. Las características faciales estaban apropiadamente contorneadas. Las formas del cuerpo de brazos, piernas, y pecho tenían la forma básica humana.
P. Schumacher
Nota: Schumacher está hablando originalmente de la topografía de un cuerpo. Otros sindonólogos posteriormente hablan de la distancia entre la sábana y el cuerpo.
Nota: No estamos diciendo que todas y cada una de las transformaciones individuales deban ser lineales, sino que el conjunto de todas ellas lo sea.
Hemos comparado el perfil de una cabeza, según las observaciones de Jackson, Jumper y Schumacher. Otros sindonólogos dicen que la imagen no representa la topografía, sino la distancia entre sábana cuerpo.
Se puede comprobar que la intensidad final tampoco guarda las proporciones con la función distancia Sábana-Cuerpo (línea azul en la figura de la segunda transformación)
En realidad, existirían otras transformaciones que no hemos tenido en cuenta:
- Las distorsiones de tamaño que se producirían en la sábana, y que vimos en la segunda parte
- Hacer una fotografía de la sábana, generar el negativo, y de ahí producir la imagen positiva que se mete finalmente en el analizador de imágenes.
No tenerlas en cuenta es lo mismo que suponer que reproducen fielmente la función de entrada que tengan, sin deformaciones, distorsiones, ni desproporciones.
Así pues, a partir de la hipótesis de formación de la imagen, se llega a un resultado que no es coherente con la representación en 3D que hace el VP8. Las conclusiones posibles son,
- Una: si la imagen del VP8 es coherente con el volumen de un cuerpo, y si la imagen se produjo como sostienen los sindonólogos, entonces hay que concluir necesariamente que la persona de la sábana estaba deformada.
- O dos: admitir que al menos una de las dos proposiciones, o incluso las dos (“hipótesis de formación”, o “representación del VP-8 es correcta”) es errónea.
Por hacer más visual cómo la hipótesis sindonológica transforma una figura tridimensional en un nivel de grises de una tela, y cómo sería representado posteriormente en 3D, he aquí un ejemplo simple.
Un óvalo, cubierto por una “sábana” (con forma de parábola):
- Que sea una pintura o dibujo justifica que no haya grandes distorsiones en 2D, y las que hay sean atribuibles a la poca pericia del artista.
- Genera una imagen en 3D con al menos tan “forma humana básica” (P. Schumacher dixit) como la imagen de la Sábana Santa
Esta entrada forma parte de una serie dedicada a la Sábana Santa. Se recomienda leer las partes precedentes a ésta.
La sábana milagrosa:
0. Introducción
1. La formación de la imagen
2. Distorsiones en 2D
3. La representación en 3D
4. Apéndice: absorción de luz en un medio saturable
Otro ejemplo de proyecciones ortogonales son las fotografías, donde la película (o el sensor CCD en las digitales), registra una proyección generada por la lente del escenario que está fotografiando.
Por eso se puede por ejemplo, coger una pelota, fotografiarla junto a una regla, y usar la regla para medir su tamaño en el ordenador.
Las dimensiones de un objeto en el espacio se describen por 3 variables (x,y,z). Una “proyección” lo que hace es suprimir una de estas variables proyectando la sombra del objeto sobre el plano definido por las otras dos, para ignorar esa información, y trabajar sólo con la sombra producida. Equivalentemente, y por hacer la analogía con la Sábana Santa más evidente, también podemos imaginar que del objeto salen rayos de luz paralelos hacia un plano, y trabajamos con la dimensión y orientación de la silueta luminosa dejada en él.
En el caso de la Sábana Santa, la tercera dimensión eliminada es la vertical, pero que sin embargo, los sindonólogos recuperan cuando tratan con los distintos niveles de oscuridad de la imagen.
Nótese además como el becario, o bien tiene sus partes nobles a la altura del ombligo, o la postura a adoptar para coincidir con la imagen de la Sábana Santa resultaba demasiado forzada como para mantenerla
Un ejemplo clásico son los mapamundis, donde se intenta representar en una hoja plana la geografía de nuestro planeta [casi]-esférico.
Es inevitable que los continentes aparezcan deformados. Según la representación que se escoja, serán unos u otros, pero es inevitable.
Se pueden hacer medidas “on line” de la sábana, en esta web. Basta pinchar en dos puntos, y la web (que según dicen tienen la imagen calibrada) nos da la distancia entre ambos puntos.
La resolución es de 1.9 milímetros por píxel. Es recomendable hacer la misma medida varias veces, ya que es difícil pinchar con el ratón dos veces en el mismo punto. Es difícil que dos personas hagan la misma medida exacta, pero si hacen varias, y calculan la media y desviación, entoces los valores sí deberían ser muy similares.
(Para tallas de calzado en otros países, ver esta tabla.
Y aquí, para calcular tallas y longitudes del pie)
Nótese que hemos escogido sólo una parte de la frente, que además es la parte menos curvada de ella. Hemos supuesto el caso en que la sábana está sobre la cabeza, y cae por acción de la gravedad sobre ella, de forma que la zona de la frente que hemos considerado es la que aproximadamente estaría en contacto directo con la sábana.
Esta entrada forma parte de una serie dedicada a la Sábana Santa. Se recomienda leer las partes precedentes a ésta.
La sábana milagrosa:
0. Introducción
1. La formación de la imagen
2. Distorsiones en 2D
3. Representación en 3D
4. Apéndice: absorción de luz en un medio saturable
A pesar de la actual preferencia de Fanti, la radiación que emana del cuerpo sigue jugando su papel en la hipótesis de la descarga eléctrica. No se ha descartado la emisión de radiación. Lo que ha hecho es añadir la descarga eléctrica a la hipótesis, en parte para explicar el hecho de que los pelos aparezcan en la imagen como si se hubieran empleado cantidades industriales de laca y gomina, en vez de estar colgando hacia atrás. La razón: en presencia de un campo electrostático, los pelos se erizan.
Aquí, el sindonólogo Oswald Scheuermann en plena investigación de la hipótesis de la descarga de corona.
Así que, resumiendo, el mecanismo de formación de la imagen más extendido es más o menos el siguiente:
- El cuerpo emite una radiación luminosa (es decir, electromagnética en el rango del visible).
- La radiación (a lo mejor en combinación con una descarga eléctrica) afecta a la parte más superficial de las fibras de la tela. - La tela se oscurece (o “amarillea”), dando lugar a la imagen.
- La distancia entre el cuerpo y la sábana afecta a la cantidad de radiación que recibe la tela, y así la cantidad en que se ha oscurecido la sábana se puede relacionar con la distancia a la que tenía el cuerpo en ese punto, y por ende con la “tridimensionalidad” ó “volumen” que se observa al representar en 3D los niveles de “oscuridad” de la imagen.
Vayamos por partes, como las integrales.
Asumiremos el milagro de la emisión de radiación energética intensa pero breve. No vamos a ver si eso es o no posible, sino a desarrollar la hipótesis, tirar del hilo, ver qué pasaría con la radiación de ser posible tal emisión milagrosa, y un poco ver cómo ha sido el proceso que los sindonólogos han seguido para ir modificando la hipótesis a medida que las leyes de la física decidían no colaborar.
La propagación de la radiación electromagnética tiene sus reglas. Estas reglas las llamamos “óptica”, y sirven por ejemplo, para saber cómo recoger la luz que emana de un objeto, para formar una imagen de él en otro lugar. Los dispositivos que hemos inventado para ello son las “lentes”. Pero junto con el santo cuerpo, no se envolvió ningún tipo de lente, ni nada que pudiera actuar como tal. ¿Qué le ocurrirá entonces a la radiación emitida por el cuerpo? Pues depende de lo que supongamos.
Empecemos por suponer lo más sencillo, natural, y para nada milagroso (suficiente milagro es ya que un cuerpo emita una extraña radiación): cada punto del cuerpo emite radiación en todas direcciones. Lo hace el Sol. Lo hace una bombilla cualquiera. Es lo habitual: ninguna molécula, o átomo tiene noción de qué es arriba, abajo, izquierda, derecha, frente o atrás: cualquier dirección es buena para emitir un rayo de luz, y por eso se emite en todas las direcciones.
El resultado es que sería imposible obtener una imagen nítida y enfocada.
Cuando se quiere proyectar una imagen de un objeto emite (o refleja) luz en todas direcciones, una lente recoge la luz que sale de cada punto del objeto, y la concentra de nuevo en un sólo punto en una pantalla donde vemos la imagen final proyectada. Pero sin lente, a cada punto de la pantalla le llegan rayos desde todos los puntos del objeto que emite luz. Cada rayo lleva información acerca del punto del que salió. Pero sin la lente, esta información se entremezcla, y es imposible separarla para obtener una imagen enfocada.
Un pequeño experimento casero. Busca y encuentra:
-Una linterna
-Un papel blanco
-Una cartulina negra
-Un folio blanco
-Una lente
Recorta un muñeco en la cartulina. Pega el papel blanco detrás de la cartulina. Colócalo justo en la ventana de la linterna, enciéndela, y dirige la luz hacia el folio blanco: sólo verás una mancha de luz. La luz de la linterna, al llegar al papel, se dispersa y sale en todas direcciones. Es como si el muñeco recortado fuera el cuerpo, y el folio la sábana.
Como ya hemos dicho, no se ve nada porque la luz sale del papel en todas direcciones, y todos los rayos se entremezclan al llegar al folio.
Si ahora colocas la lente entre medias, al acercarla o alejara en algún punto conseguirás obtener la imagen del muñeco (aunque invertida). La lente recoge la luz, y la vuelve a concentrar para formar la imagen.
Una cosa más que se puede comprobar, es que sin la lente, al acercar la linterna al folio en blanco, conseguirás ver el muñeco sólo cuando hagas contacto entre la linterna y el folio. Al hacer contacto, estás evitando que la luz se disperse antes de tiempo, y por eso la imagen se puede ver en el folio: a cada punto del folio sólo le llega luz de un solo punto de la fuente de luz: la imagen sale enfocada.
¿Qué le ocurre a la imagen de la Sábana Santa? Toda ella está enfocada. Sin embargo, sólo aquellas zonas en que la sábana tocaba el cuerpo podría haber dejado una imagen así. En cambio, aquellas que no estaban en contacto, como mucho podrían haber dejado únicamente una mancha difusa, sin que se aprecie detalle alguno: la punta de la nariz podría verse, pero de los ojos sólo se vería un tenue manchurrón. Se vería bien la rodilla, pero no la espinilla, sino un manchurrón más alargado y más gordo que la pierna que aparece.Y de la imagen dorsal en contacto estaría la cabeza, parte de la espalda, el culo, y los talones, pero no las piernas, ni las plantas de los pies. Respecto a los brazos y codos, que tampoco estarían en contacto con esa parte de la sábana, los agujeros en la tela debidos a los incendios que sufrió han eliminado esa parte del dibujo, pero me atrevo a decir que estaban ahí.
Esta imagen representa cómo estaría envuelto el cuerpo, según los sindonólogos. Comprueba como las zonas de no-contacto aparecen en la imagen de la sábana.
Según los sindonólogos, el rigor mortis evitaría que los brazos se cayeran por gravedad, al igual que las piernas se mantendrían flexionadas.
Las piernas flexionadas se deben a la postura que tradicionalmente se asume y pintan los artistas en la crucifixión. Ahora falta que nos cuenten si hubo que partirle los brazos a Jesús para ponerle en esa postura, dónde están las marcas correspondientes, y por qué los brazos no intentaron volver a su posición anterior, debido a ese mismo rigor mortis.
Por otro lado, una radiación en todas direcciones también tendría que haber dejado alguna mancha proveniente del lateral del cuerpo. Y no hay ninguna.
Así que una radiación que se dispersa en todas direcciones no parece ser posible para haber generado la imagen.
Hemos llegado pues, al primer obstáculo. Podemos suponer que la óptica dejó milagrosamente de funcionar en aquel momento. O podemos no ser tan drásticos, y complicar sólo un pelín más el milagro, llegando a la misma conclusión que los sindonólogos: la radiación se emitía en una única dirección, la vertical. Así evitamos el problema de la nitidez de la imagen, y también de la falta de imagen lateral.
No entraremos a evaluar si existe un mecanismo que hiciera que la luz se emitiera sólo en vertical, como tampoco si hay un mecanismo que hace emitir la radiación al cuerpo. Es parte del milagro que hay que asumir (y posteriormente demostrar si la condición imaginada produjera los resultados observados)
Si los rayos de luz de la linterna fueran todos exactamente paralelos, la imagen final tendría el mismo tamaño que la forma original. Como no lo son, la imagen aumenta de tamaño al alejar la linterna del folio que sirve de pantalla. Se supone que esto no le pasa a la imagen de la sábana santa.
En esta prueba hay que obviar también la no uniformidad de la intensidad de la luz, que es debida a la propia linterna. Se supone que el cuerpo emite de forma uniforme. Sólo estamos comprobando bajo qué circunstancias aparece una imagen bien definida
¿Tenemos entonces por fin una coherencia entre nuestro milagro supuesto y lo que se aprecia en la sábana? No tan rápido, porque la forma de propagación de la radiación afecta a cómo ésta pierde intensidad según avanza, lo cual se relaciona con el detalle y contraste de la imagen final (y también con cómo se genera posteriormente la imagen en 3D)
El primer caso (radiación difusa), en el caso más ideal, se llama “onda esférica”:
Una fuente “puntual” (infinitamente pequeña) emite luz. Por la simetría geométrica de la situación, no hay direcciones especiales: no hay diferencia entre derecha, izquierda, arriba, abajo, delante o detrás, por lo que todos los rayos salen en todas direcciones. La intensidad de la radiación se reparte entonces en torno a una esfera, cuyo centro es la fuente de la radiación.
Para entender más claramente por qué y cómo varía la intensidad al propagarse la luz en una onda esférica, supón que los rayos de luz son en realidad pequeñas bolitas (si a alguien esto le suena a mecánica cuántica, que no se asuste, que es lo más lejos que vamos a llegar). En un instante de tiempo dado, la fuente de luz puntual emite por ejemplo, 10000 de estas bolitas. Como ninguna sabe si existe una dirección especial, y todas viajan a la misma velocidad, se ordenan de forma homogénea, formando una esfera alrededor de la fuente. Las bolitas están muy juntitas, de forma que si colocas una copa al lado, y cuentas cuantas bolitas puedes recoger en ella de una sola vez, te saldrá un número determinado (10 por ejemplo).
Al cabo de un tiempo, las bolitas que se desplazan a la velocidad de la luz han avanzado en línea recta, alejándose todas de la fuente, y ahora forman una nueva esfera con un radio mayor. La superficie de esta esfera es también mayor, pero el número de partículas es el mismo (10000), por lo que ahora están más separadas. Si colocamos la misma copa de antes, a ver cuantas bolas recogemos de una vez, resulta que en vez de 10, son un número menor, 5 por ejemplo.
Es decir, nuestra copa (que hace las veces de detector), abarca sólo una pequeña parte de la superficie de la esfera que forman las bolitas de luz (fotones), y cuenta “cuantas bolitas hay en esa pequeña región de la superficie”. Esto es la intensidad: el número de fotones [que cada segundo] llegan a un área fija determinada. Como al propagarse la luz el tamaño de la esfera que forman los fotones aumenta, pero el número total de fotones es constante, eso quiere decir que cuanto más lejos pongamos el detector, menos fotones llegarán al área determinada por éste: la luz ha perdido intensidad.
Si el número de fotones por segundo que emite la fuente es I0, y la superficie de una esfera de radio r es 4πr2, los fotones se reparten uniformemente, y en cada unidad de superficie hay I0/(4πr2) fotones. La intensidad decae de forma inversamente proporcional al cuadrado de la distancia. Lo cual a la mayoría debería sonarle familiar.¿Qué ocurre en el caso de la radiación vertical? Ese caso corresponde a lo que idealmente se llama “onda plana”, o “radiación colimada”: los fotones se reparten en el área determinada por un plano que es perpendicular a la dirección de propagación. Los fotones avanzan ahora paralelos entre sí, por lo que no se van a separar ni acercar, y el área del plano que forman será siempre el mismo. Si colocamos la misma copa del ejemplo anterior para recoger fotones, dará igual colocarla antes o después, porque siempre recogerá el mismo número de fotones.
Las ondas planas son típicas de un láser: sus rayos de luz son (casi) perfectamente paralelos, por lo que apenas pierden intensidad. Se puede apuntar con un láser a distancias lejanas (50-100 metros), y observar el punto con buena intensidad, y un tamaño un poco mayor que si apuntara a un objeto cercano. Si se compara con la luz de una linterna, o del flash de una cámara de fotos, el haz de luz alcanza una corta distancia (5-10 metros) porque pierde intensidad, debido a que los rayos de luz se están separando demasiado rápido, pero por otro lado da lugar a que el tamaño del haz se expanda con rapidez e ilumine un área más grande
La disminución de intensidad con la distancia es más una consecuencia geométrica que una ley física. Por eso tampoco es de extrañar las coincidencias con fenómenos como fuerzas eléctricas o gravitatorias, que también dependen inversamente del cuadrado de la distancia.
Simplificando: si los rayos de luz se separan, la intensidad disminuye. Si se unen, aumenta. Las ondas esféricas separan sus rayos. Las lentes, los pueden unir y separar. Las ondas planas mantienen la distancia entre sus rayos.
Después del rollo este, llegamos a lo que realmente nos importa en nuestro caso. La propiedad de las “ondas planas” de no perder intensidad resultaría ser responsable de que no viéramos detalles en la imagen en la sábana.
Los detalles de la imagen se pueden ver debido a los distintos niveles de oscuridad en la sábana, que dan el contraste para ver ojos, barba, brazos, etc… Este contraste de oscuridad es provocado porque las fibras de la tela reaccionan más o menos (se oscurecen más o menos) según la intensidad de la radiación, debido a las distintas distancias cuerpo-sábana que la radiación recorre. Pero hemos dicho que una onda plana lleva igual intensidad, independientemente de la distancia recorrida.
Por tanto, independientemente de la distancia recorrida, a cualquier punto de la sábana le llegaría igual cantidad de radiación, y no podrían registrarse distintos niveles de oscuridad, sino que sólo se vería ¡una mancha uniforme con la silueta del cuerpo bien definida! (Matiz: siempre y cuando la sábana estuviera perfectamente plana, flotando sobre el cuerpo. Más adelante veremos por qué)
Tenemos entonces dos extremos: Una onda plana genera una imagen nítida, pero como no pierde intensidad, la imagen no tiene el contraste necesario para generar detalles. Una onda esférica pierde intensidad y puede dar contrastes debidos a la distancia cuerpo-sábana, pero desenfoca la imagen.
Por supuesto, esto son casos “ideales”. Hay casos intermedios a los que algún sindonólogo intentaría agarrarse como clavo ardiendo, pero que presentan otros problemas: por ejemplo, en la emisión de una linterna, los rayos no son perfectamente paralelos y se separan unos de otros; la separación hace que la intensidad disminuya con la distancia. Si se ilumina un objeto cercano, recibirá más intensidad que si el objeto está un poco más allá. Y si está muy lejos, ni siquiera será iluminado. La forma en que varía la intensidad será más o menos fácil de calcular según cada caso.
En el segundo experimento con la linterna, veíamos la imagen recortada proyectada de forma razonablemente nítida; si os apetece entreteneros, podréis comprobar que cuanto más lejos se haga la proyección, menos intensa será la imagen… pero el problema es que la forma proyectada aumentará de tamaño.
Es decir, una solución intermedia (rayos de luz casi paralelos, o “casi colimados”) produce cambios de intensidad según avanza la luz, porque los rayos se separan. Pero por otra parte, aumenta el tamaño de la imagen, y más cuanto más lejos proyectemos. El resultado final sería una imagen del cuerpo en la sábana deformada: una nariz con un tamaño adecuado, por estar en contacto con la sábana, pero unas cuencas de los ojos agrandadas, por estar en profundidad.
Si intentamos corregir esta deformidad haciendo los haces de luz más paralelos, perdemos contraste de imagen por la menor pérdida de intensidad. Si intentamos ganar contraste con los detalles dispersando más la luz, la imagen se agranda, se deforma, los rayos de luz comienzan a solaparse, mezclarse, y se llegará a obtener finalmente una mancha borrosa, como si tuviéramos una luz emitida en todas las direcciones (como el primer caso que hemos tenido en cuenta)
De nuevo, las leyes de la física nos ponen la zancadilla. Ante esta circunstancia, los sindonólogos optan por cuadrar el círculo:
Asumir que la radiación era una onda plana (que se propaga sólo hacia arriba y hacia abajo), pero que pierde intensidad en su propagación como si fuera una onda esférica (como la inversa del cuadrado de la distancia).
Pero por si pareciera poco, además la intensidad con que sale la radiación del cuerpo obedece una “ley del coseno” un tanto peculiar: la intensidad depende del ángulo entre la perpendicular de la superficie del cuerpo, y la vertical.
La circunferencia de la anterior representa el contorno de una pierna. En cada punto, la superficie forma un ángulo Θ con la vertical. Según esta “ley del coseno sindonológica”, la radiación se emite sólo en vertical, con un valor inicial en cada punto que depende del coseno de Θ, y que disminuye su intensidad con la inversa del cuadrado de la distancia que recorre hasta la sábana.
Este añadido corresponde a unos resultados experimentales, según los cuales, la intensidad de las piernas en un corte transversal, se pueden describir con una función coseno.
A partir de ahí, sin necesidad de comprobar que otros puntos de la imagen cuerpo cumplen la misma “regla”, se asume para toda la imagen.
Sí que existe una ley del coseno [de Lambert], que en sí misma no es extraña, sino muy corriente. Se aplica tanto a superficies emisoras de luz, como a superficies que absorben esa radiación. Y es responsable, por ejemplo, de que existan las estaciones del año, y que además estén cambiadas en los hemisferios norte y sur.
Un detector tiene una superficie finita determinada y en ella inciden los fotones para “contarlos”, y así medir la intensidad. El número de fotones que va a contar, depende del área de su superficie. A mayor área, más fotones caben, y más se pueden contar. Si el área está perfectamente perpendicular respecto del haz de fotones, el detector presenta toda su área al haz, y recogerá todos los que puede. Pero si está inclinado respecto al haz incidente, presenta menos área al haz, y por tanto, recoge menos fotones. El “área efectiva” que presenta el detector, se relaciona con el coseno del ángulo que forma el haz incidente con la perpendicular del detector. El caso más extremo es cuando la superficie del detector es paralela al haz: no podrá recoger ningún fotón. Un dibujo lo deja más claro:
El eje de rotación de la tierra está inclinado 23º. Por eso vemos al Sol más alto en verano, y más bajo en invierno. También hace que los rayos en verano lleguen más perpendiculares a la superficie, y en invierno más inclinados: como resulta de la ley del coseno, con los rayos más perpendiculares la intensidad de luz solar es mayor, y se calienta más el suelo, mientras que en invierno, la mayor inclinación de los rayos calientan menos. Como estas inclinaciones dependen de la latitud, cuando en el hemisferio norte los rayos son más perpendiculares, en el sur son más paralelos, y viceversa, y por eso las estaciones están cambiadas entre hemisferios.
Si hablamos de la ley del coseno para fuentes de luz, hay que partir de que esta fuente tiene una superficie determinada. La superficie se puede imaginar como formada por infinitas “fuentes puntuales”, que emiten en todas las direcciones. Entonces, a un punto del espacio dado, llegan rayos desde todas y cada una de las fuentes puntuales. ¿Qué intensidad total llega a ese punto? La suma de intensidades desde todos los puntos emisores, teniendo en cuenta la intensidad que han perdido en el camino, y que cada rayo ha seguido un camino ligeramente distinto. Las cuentas no son fáciles de hacer, pero al final, la intensidad que llega depende, por un lado de la inversa al cuadrado de la distancia, y por otro del coseno ángulo que hay entre el punto, y el centro de la fuente:
Espero que el dibujo suene familiar. Es parecido al de la primera prueba, con la linterna y el papel para difuminar la luz. Por lo que no hace falta argumentar mucho que una estricta aplicación de la ley del coseno [de Lambert] al problema de la Sábana Santa no produciría imagen alguna: ¡ya lo hemos comprobado experimentalmente!
La diferencia entre la ley del coseno [de Lambert] y la ley del coseno [sindonológica] es evidente. La primera tiene en cuenta la dispersión de la luz en todas direcciones. La segunda, supone una emisión en una única dirección, con intensidades que varían según el ángulo entre la vertical y la perpendicular a la superficie del cuerpo. Algo, que así a bote pronto, no parece responder a ninguna ley física, que quizás sólo se pueda hacer fabricando algún material ad hoc con una geometría calculada muy exacta, y muy heterogéneo en sus propiedades para poder controlar la transmisión, reflexión y refracción de un haz de luz que lo atraviese. Desde luego, nada que exista en la naturaleza.
Sin embargo, sí se puede (y debería) introducir (y sin apelar milagros) la ley del coseno [de Lambert] para explicar variaciones de intensidad, si la aplicamos no al cuerpo, sino a la sábana: el ángulo que forma cada punto de la sábana respecto a la luz que le llega en vertical (incluso si fuera una onda plana que no pierde intensidad) proporcionaría contrastes y detalles en la imagen. Sin embargo, no he visto aún artículo alguno en que los sindonólogos dejen claro si la usan o no.
Este es el matiz que mencionaba antes: siempre y cuando la sábana tenga arrugas y dobleces para adaptarse a la forma del cuerpo, formará distintos ángulos con la luz que supuestamente llega de forma vertical perfectamente colimada. Entonces sí habría variaciones en la intensidad que absorbe la sábana, pero que responderían a los ángulos entre sábana y haz de luz, y no a la distancia sábana-cuerpo.
Si estuviera totalmente plana (algo imposible), entonces cada punto de la sábana formaría siempre el mismo ángulo respecto a la luz, no habría variaciones de intensidad absorbida, y no habría contrastes.
Hay tanto motivo para suponer tal “ley del coseno sindonológica”, como para asumir que una radiación misteriosa se crea en un cuerpo, que esta radiación es vertical, y a la vez pierde intensidad con la inversa del cuadrado de la distancia: ¡Estamos hablando de un milagro! Es un fenómeno nuevo que la ciencia aún no ha descubierto
“aplicando el principio de mínima suposición de la navaja de Occam, se debe simplificar la situación, y seleccionar los hechos más relevantes”Giulio Fanti, sindonólogo (2005)
Por lo visto, la aplicación de la navaja de Occam a la Sábana Santa nos deja con:
1.- Una radiación misteriosa emitida por un cadáver…
2.- … que se propaga sólo en vertical sin el uso de lentes o artefactos…
3.- … que pierde intensidad como si se propagara en todas direcciones…
4.- … y que la intensidad que sale del cuerpo cumple una ley del coseno que nadie antes había descubierto.
Un tanto peculiar la forma de usar la navaja, sin duda.
